Block-Structured
AMR for Fluid Structure Interactions
In this study, an immersed boundary (IB) approach on the basis of moving
least squares (MLS) interpolation is proposed for analyzing the dynamic
response of a rigid body immersed in incompressible flows. An improved mapping
strategy is proposed for a quick update of the signed distance field. A CIP–CSL
(constraint
interpolation profile - semi-Lagrangian)
scheme with compact stencils is adopted for the convective part in momentum
equation. Fluid-structure
interaction problems can be solved by either the weak or the strong coupling
schemes according to the density ratio of the solid and fluid. This research is
based on our previous research on block-structured adaptive mesh refinement
(AMR) method for incompressible flows (Liu and Hu, J. Comput. Phys., 359 (2018), 239-262).
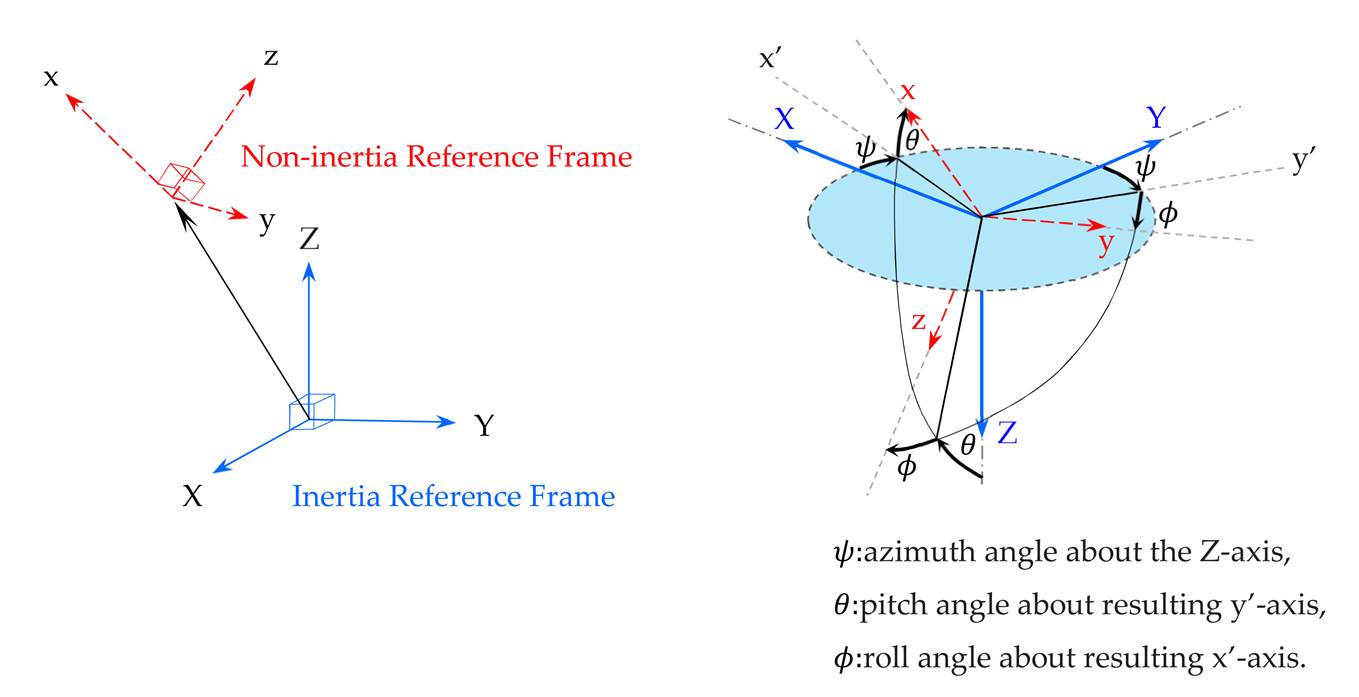
Fig. 1 (a) Definition of the
non-inertia and inertia reference frame and the Euler angle.
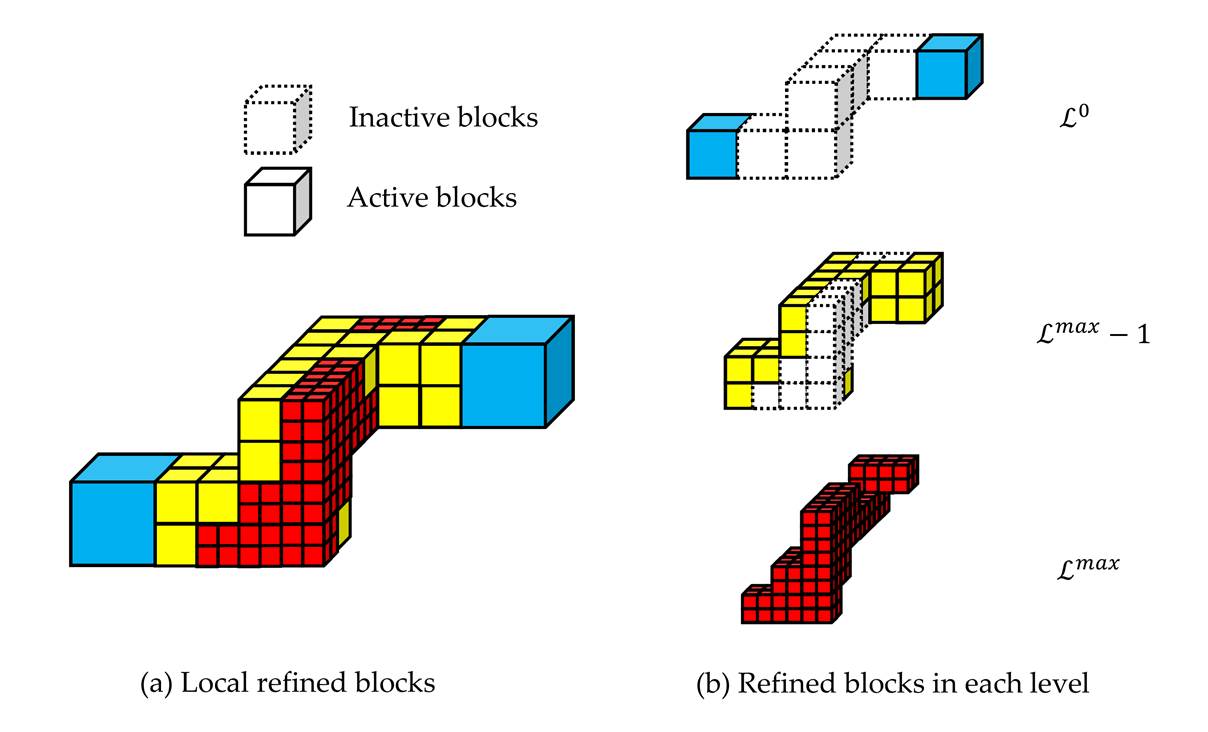
Fig. 2 3-D
Blocks and its topological structure.
Vortex Induced
Vibration of a Circular Cylinder
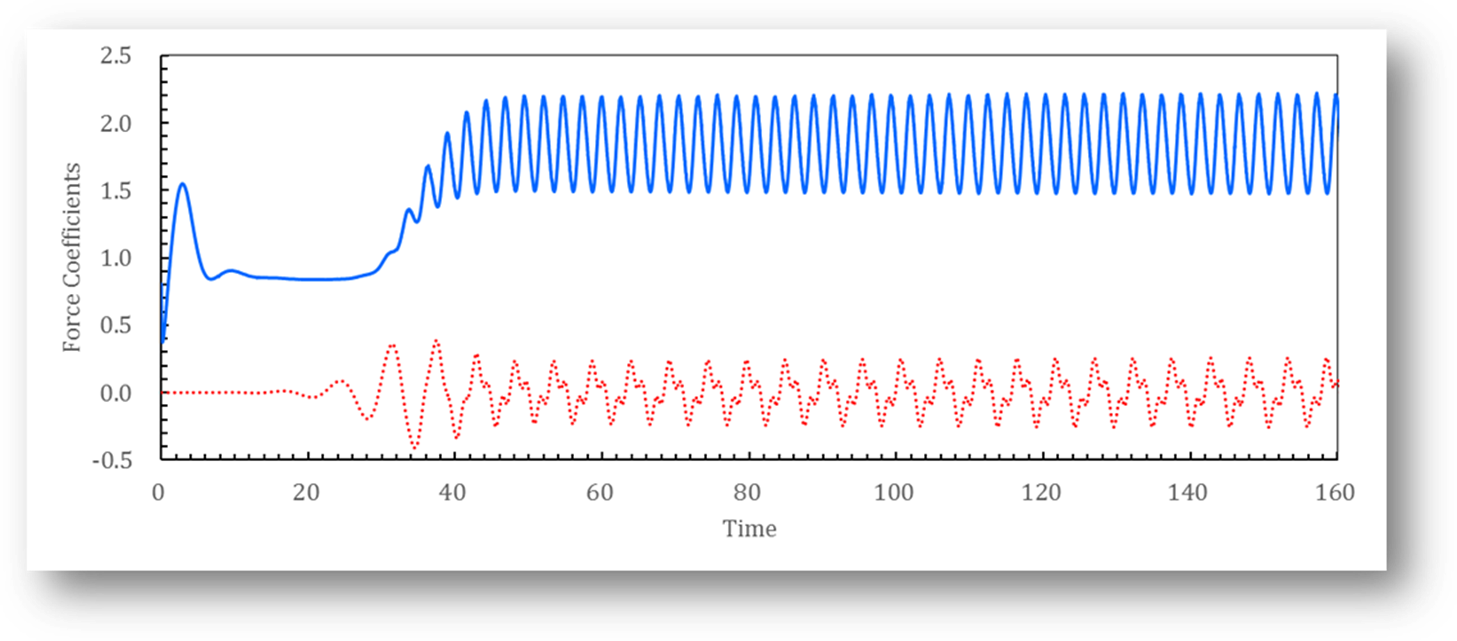
Fig. 3 Time
evolution of the drag coefficients (
) and lift
coefficients (
) for flow over
a freely vibrating circular cylinder (
, 
), –: ; ∙∙∙∙∙: .
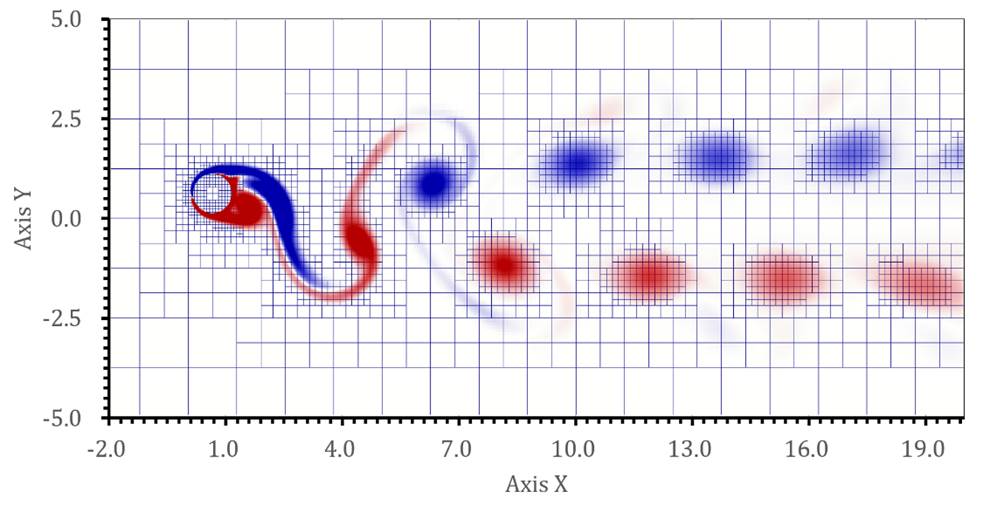
Fig. 4 Vorticity
contours of flow past a freely vibrating
circular cylinder (, 
).
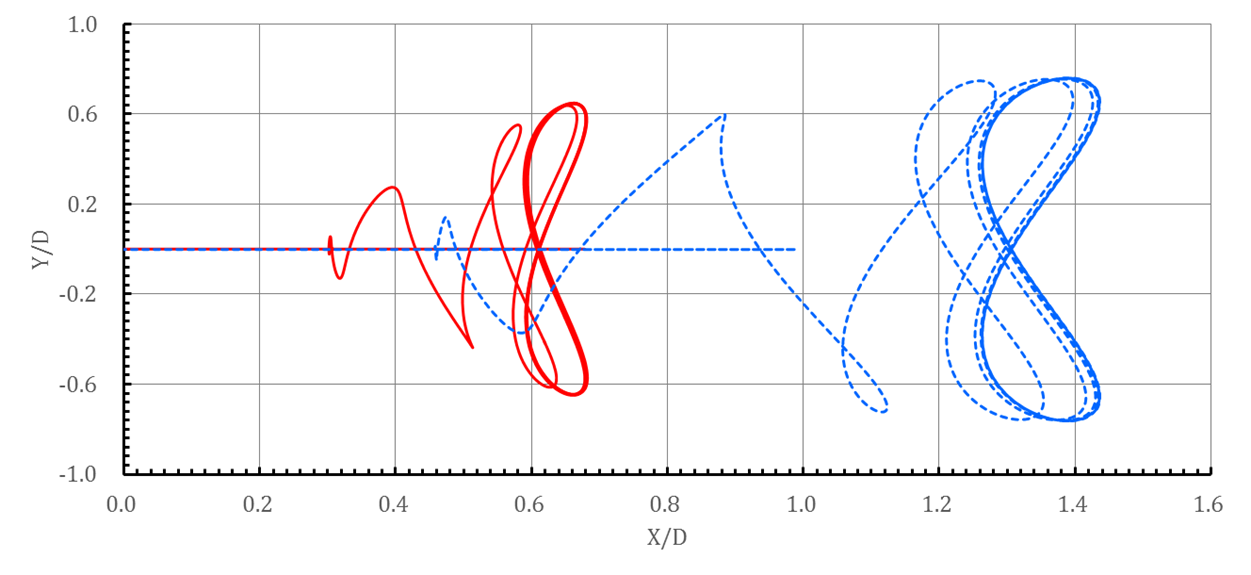
(a)
Displacement curves
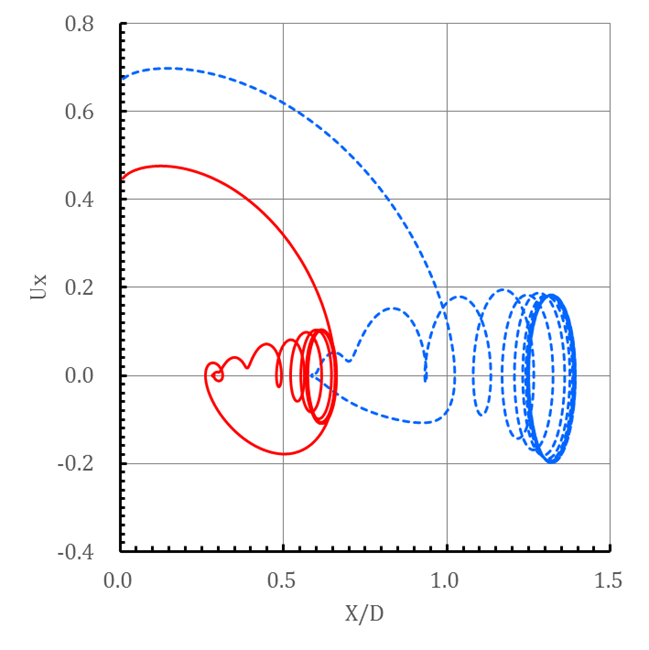
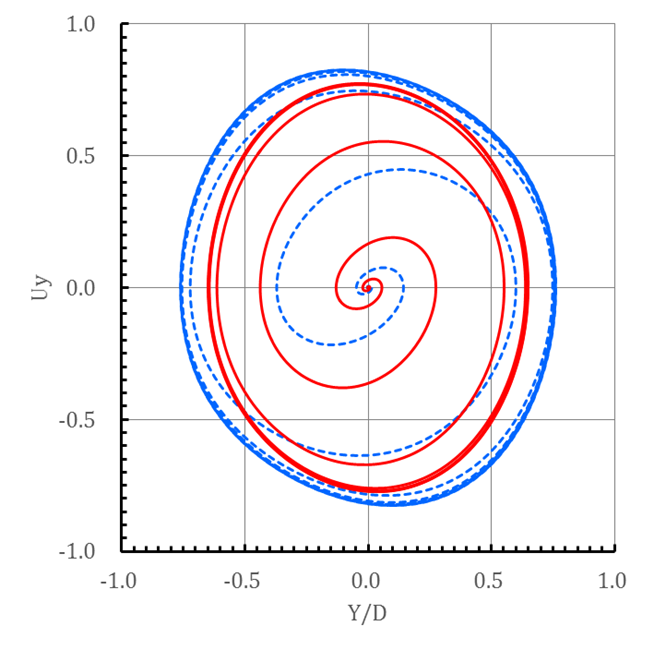
(b)
, and 
curves
Fig. 5 Displacement
and velocity response for freely vibrating
circular cylinder in free-stream () –:
;- - -:
.
Flow past a Rotational
Galloping Rectangle
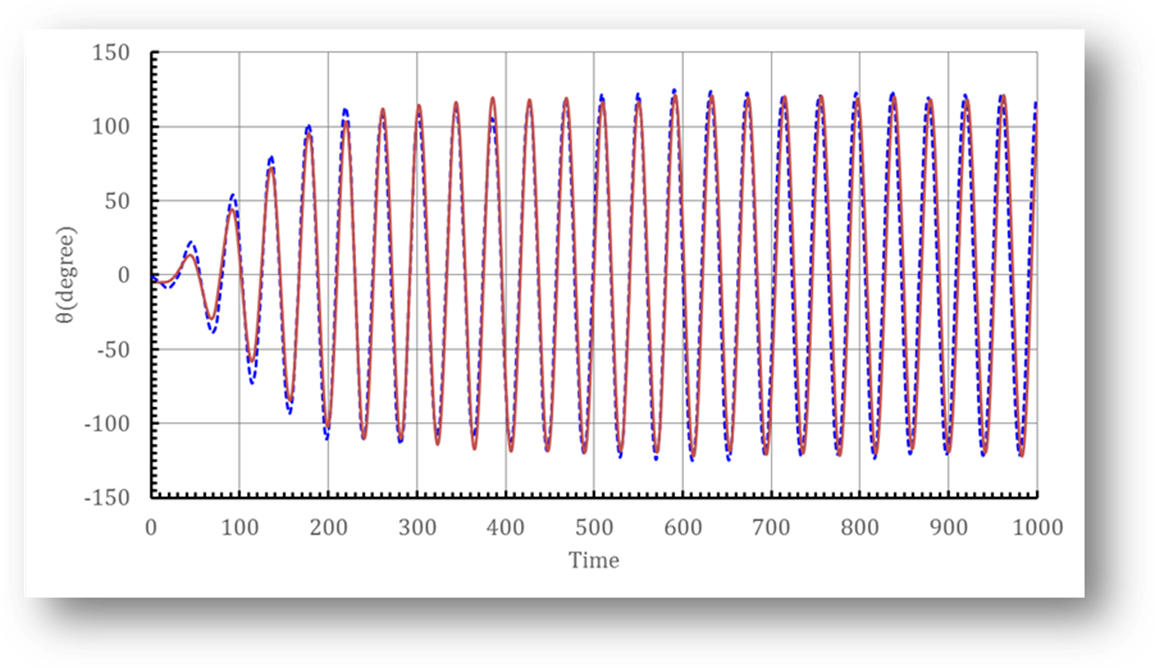
Fig. 6 Time
evolution of the pitch angle (
) for rotational
galloping square
cylinder (, 
, 
,
). –: Present results; ‑ ‑ ‑: results of Yang and Stern.
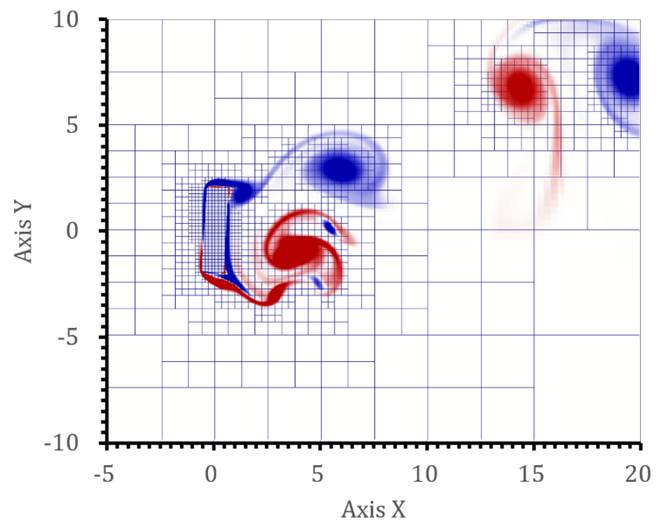
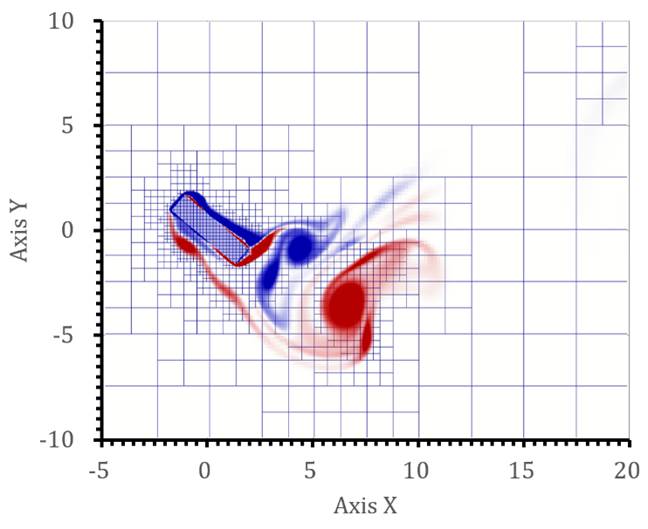
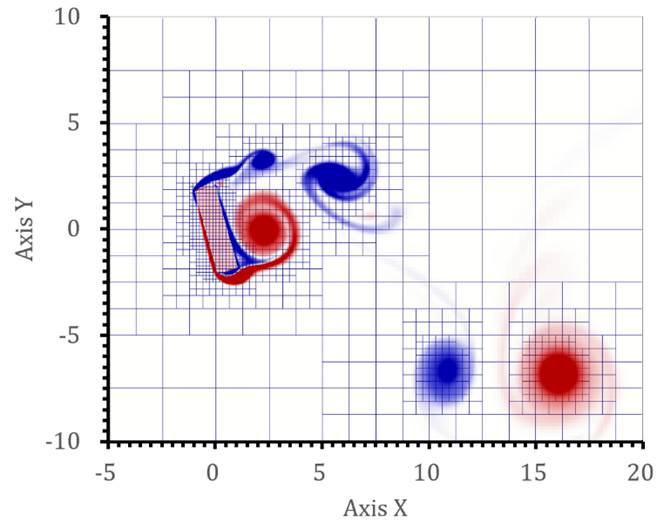
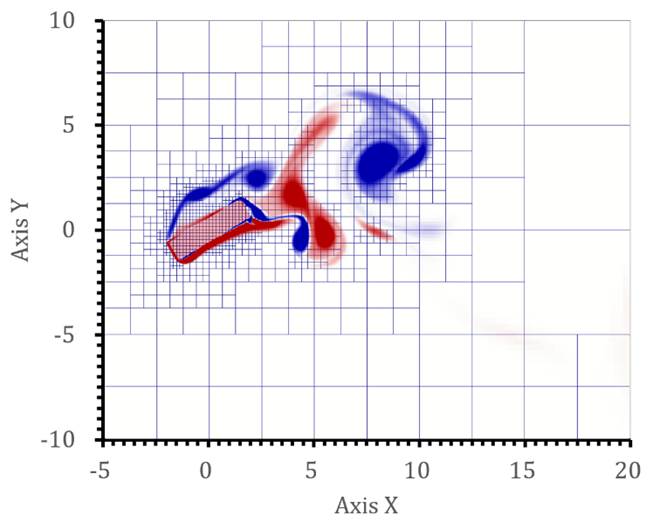
Fig.
7 Vorticity
contours in different pitch angle () for flow over
rotational galloping square cylinder (, , ,).
Freely Falling Rectangular
Plate
Fluttering Mode
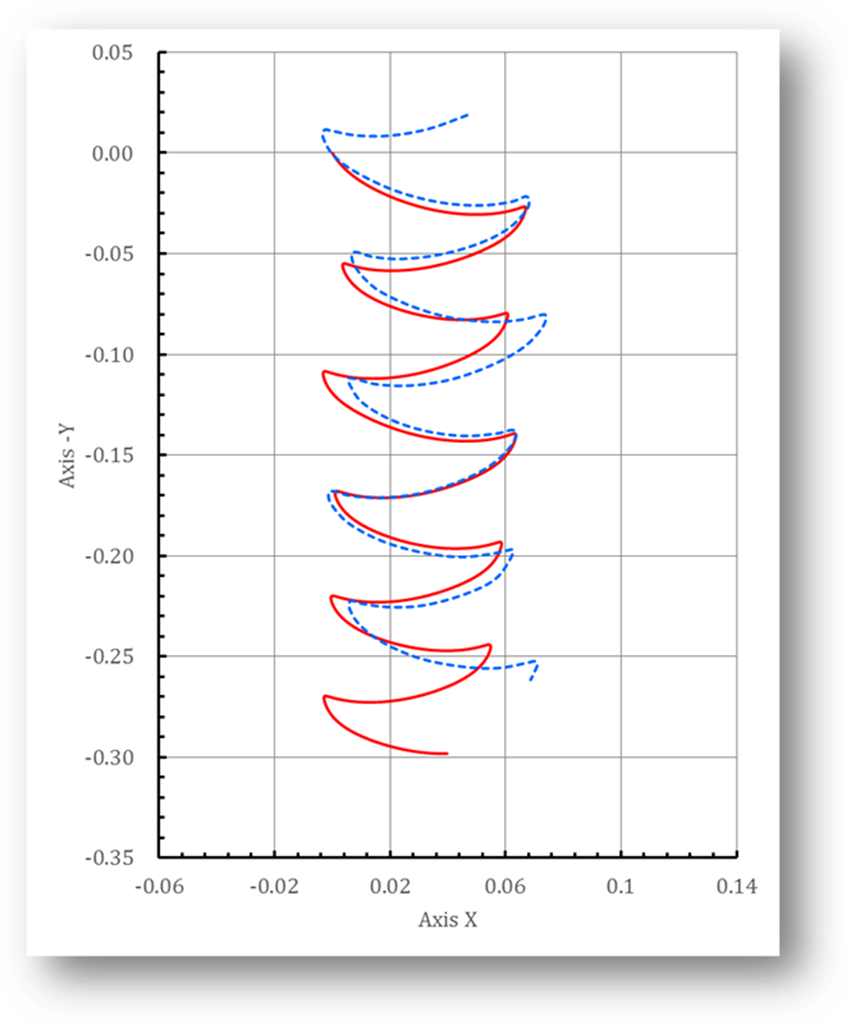
Fig. 8 Trajectory of the mass center for freely falling plate
with fluttering motion. –: present simulation, ‑ ‑ ‑: results of experiment.
(a)
,
(c)
,
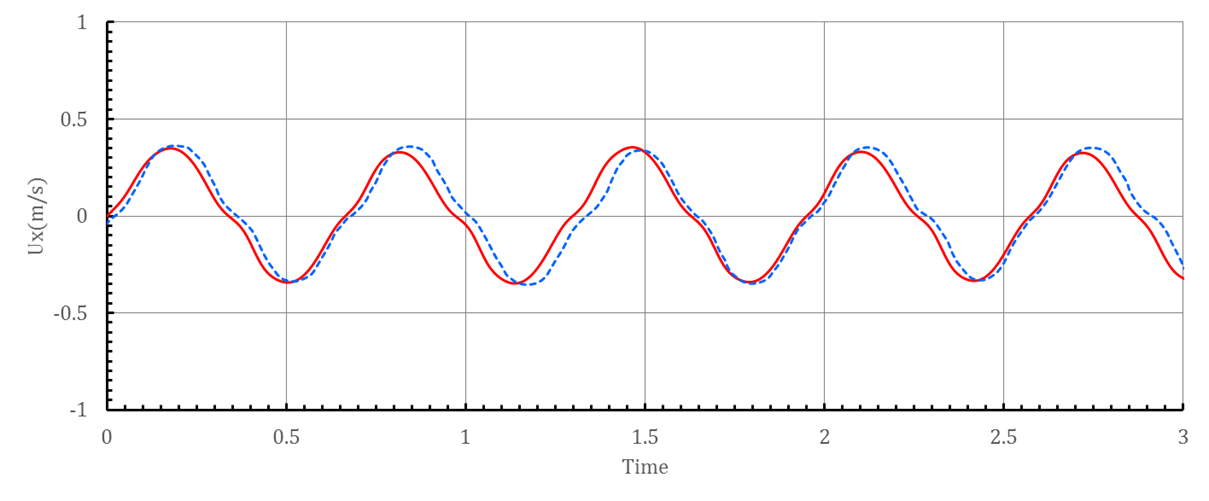
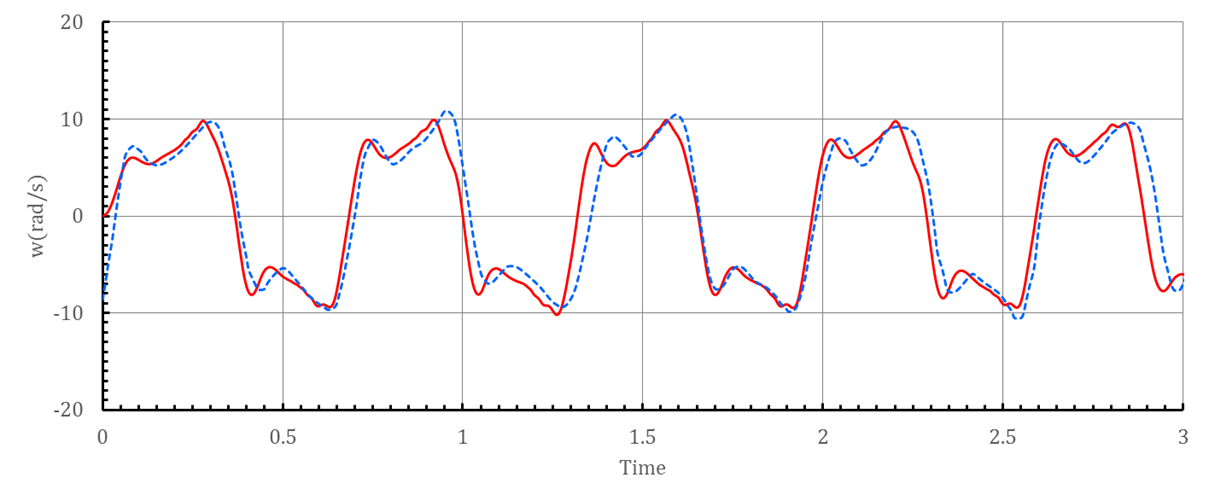
Fig. 9 Transverse velocity and rotational velocity varying with
time,–:
present simulation, ‑ ‑ ‑: results of experiment.
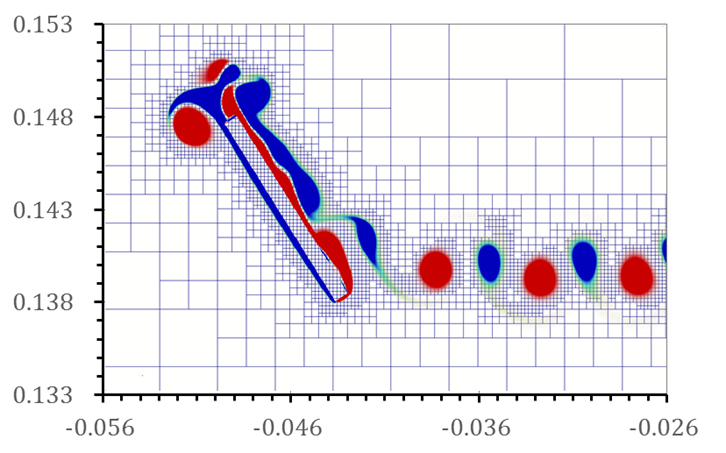
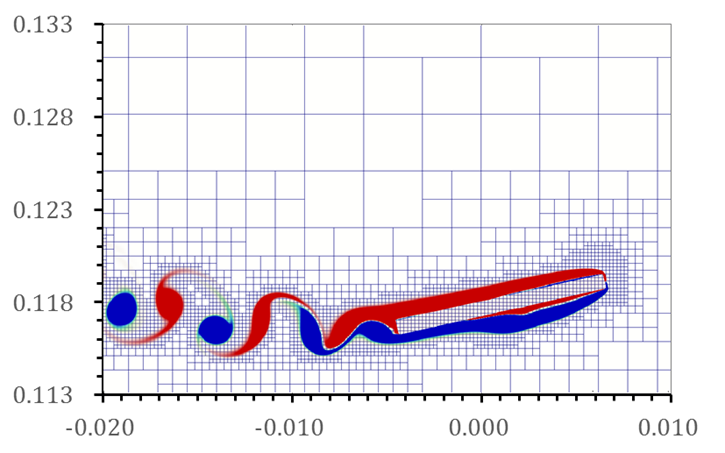
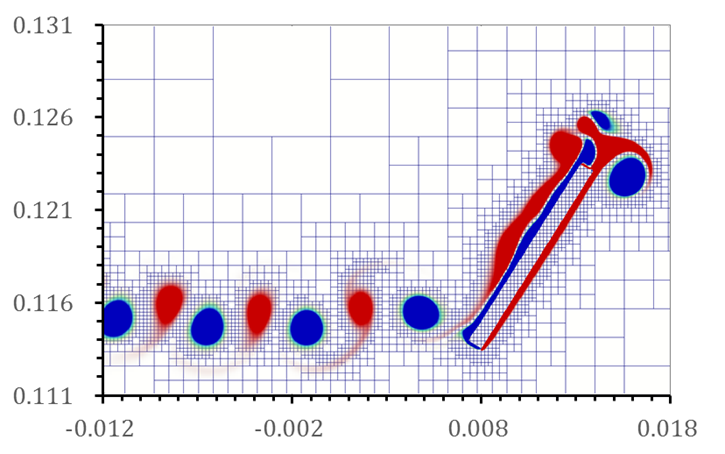
Fig. 10 Snapshot of vorticity contours for freely falling
rectangular plate with fluttering motion.
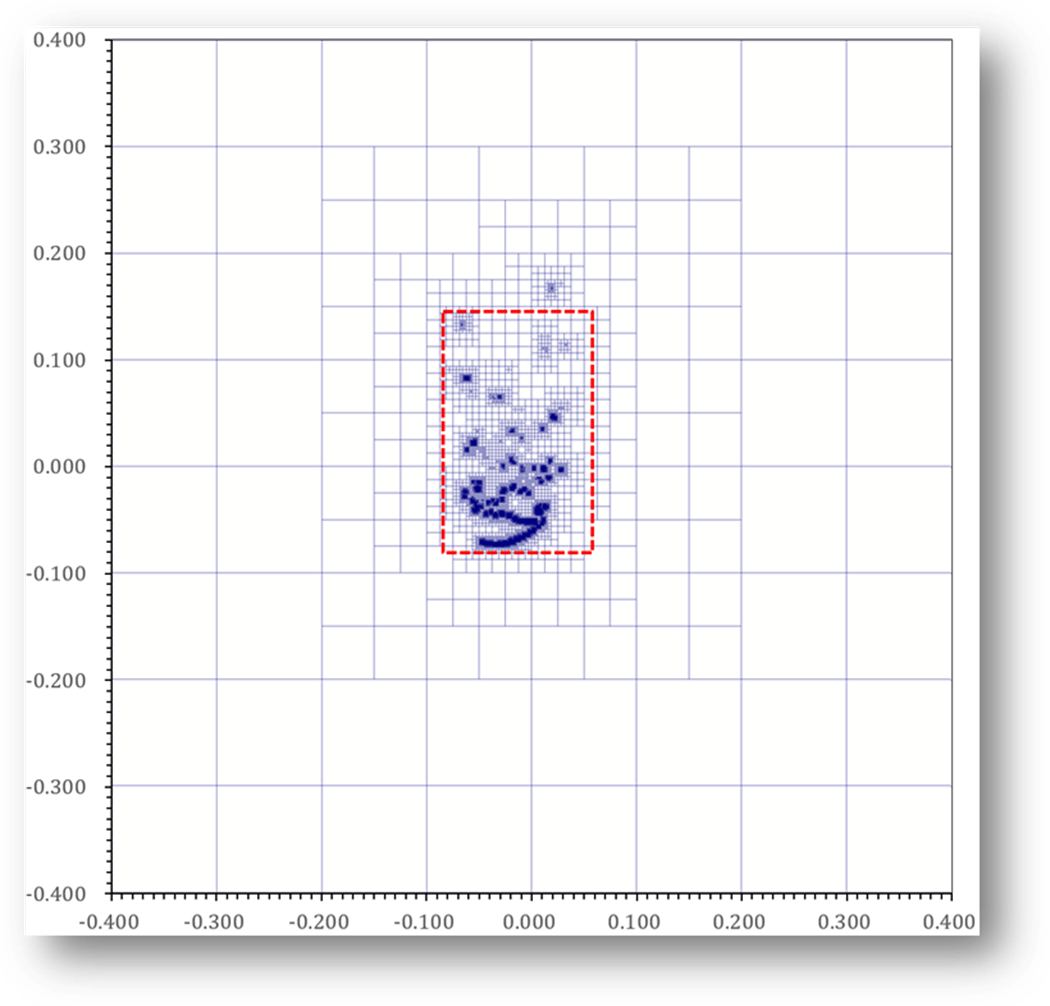
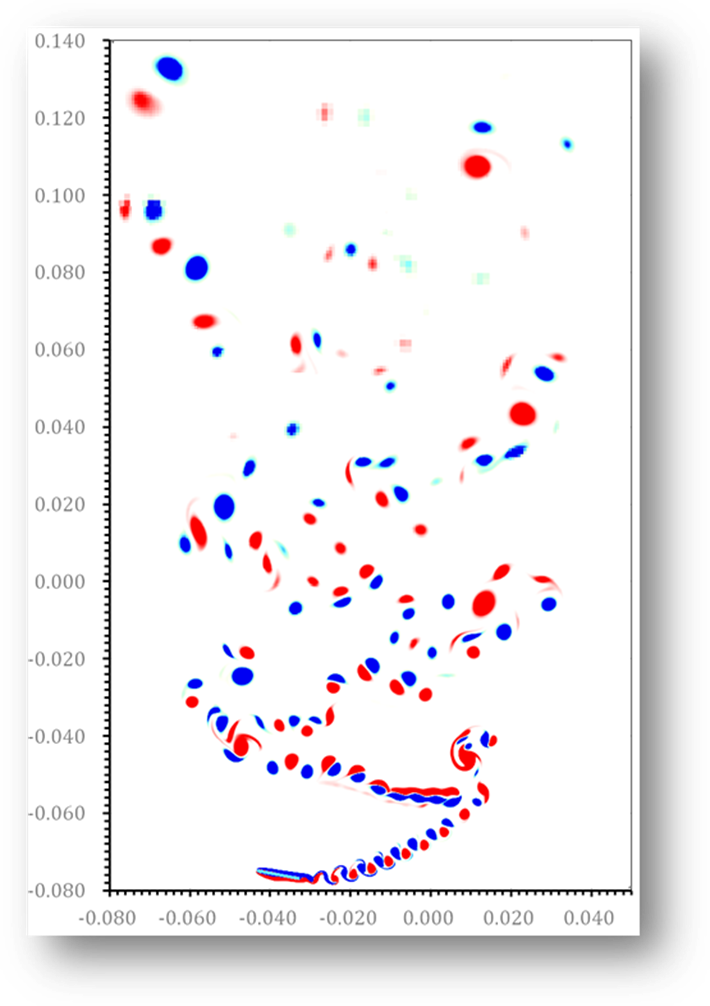
Fig. 11 (a) Blocks and vortex structure for the test of freely
falling rectangular plate with fluttering motion (
)
Tumbling Mode
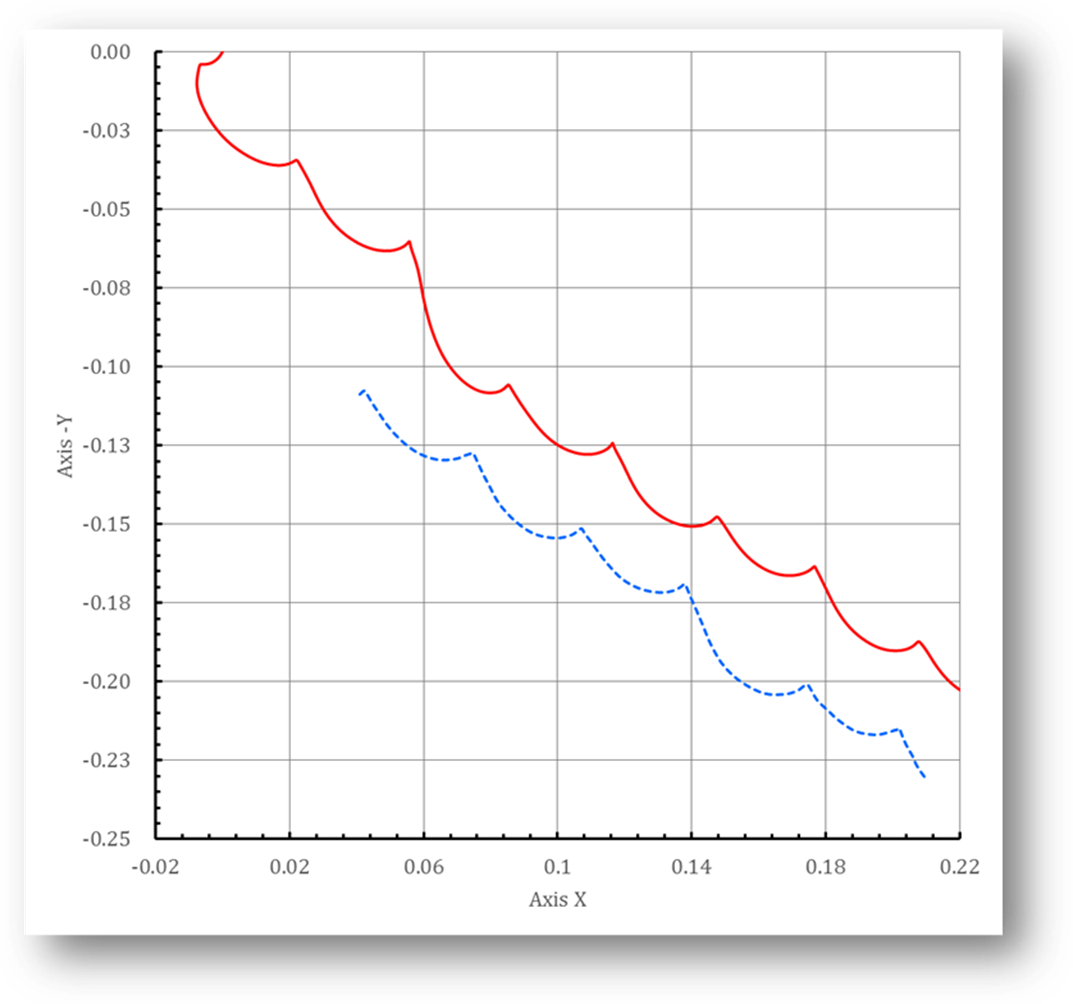
Fig. 12 Trajectory of the mass center for freely falling plate
with tumbling motion. –: present simulation, ‑ ‑ ‑: results of experiment.
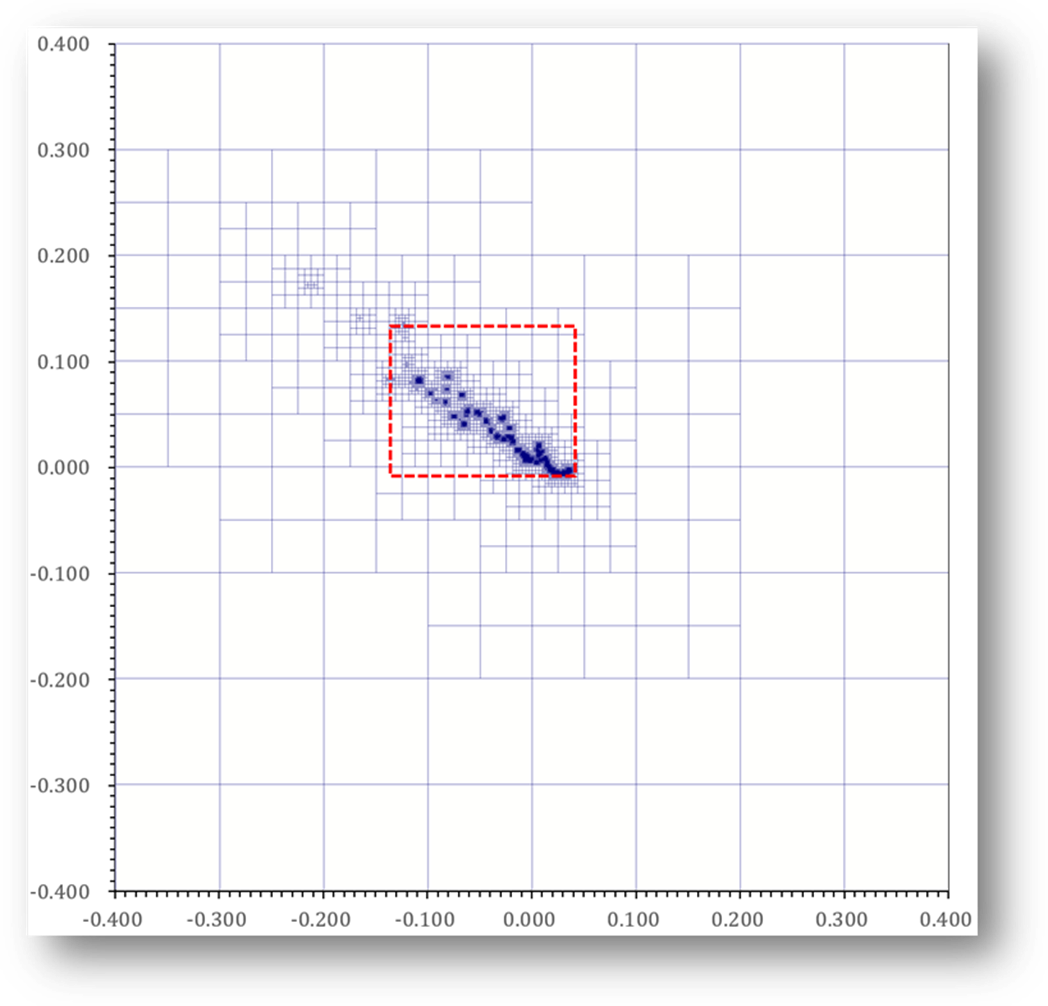
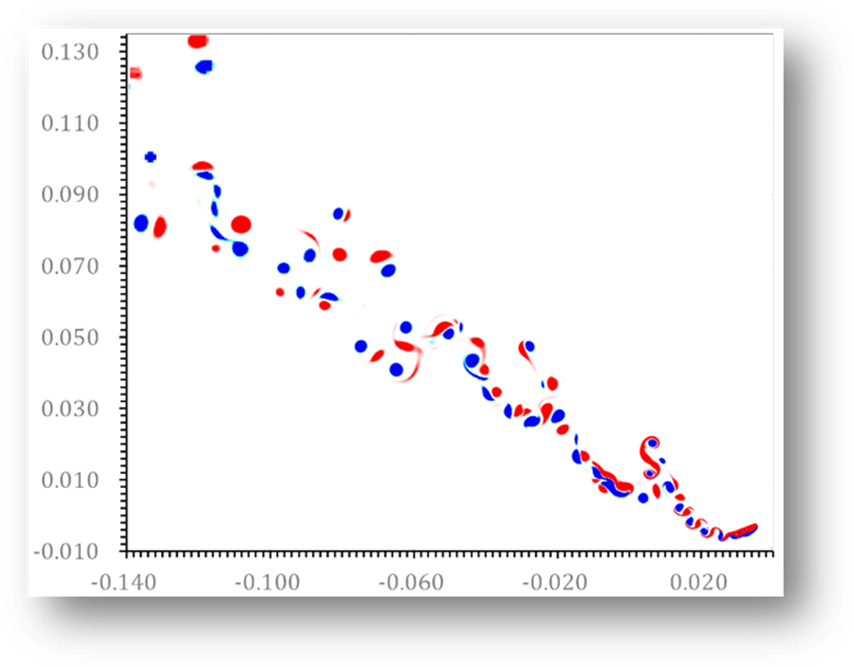
Fig. 12 (a) Blocks and vortex structure for the test of freely
falling rectangular plate with tumbling motion (
).
Reference
C. Liu*, C.
Hu, Blocked-Based Adaptive Mesh Refinement for Fluid Structure Interactions in
Incompressible Flows, submitted.