Block-Structured
AMR for Incompressible Flows
In
this study, a multi-moment finite volume method (FVM) based on block-structured
adaptive Cartesian mesh is proposed for simulating incompressible flows.
Highlights
exist in three aspects. First, it is the first endeavor to extend multi-moment
FVM to the block-structured AMR for simulating the incompressible flow
problems. Second, to preserve flux conservation, a prolongation approach by
using the idea of CIP method is proposed for filling the SIA and VIA in newly
created cells. Present conservative prolongation is motivated by C. Chen et al.’s
work, in which PV (corner point) and VIA are used to build the
multi-dimensional interpolation. In this study, SIA and VIA are employed for
the prolongation with the assistance of the multi-dimensional Lagrange
polynomial interpolation (LPI) method. Third, a fast algorithm is proposed to
generate the coefficient matrix of the Laplacian operator by regarding the
adaptive mesh as unstructured topology. For multi-dimensional problem, the
linear or quadratic connections can be built by repeating 1D interpolation
among the points in different refined levels. Compared with other similar
approaches, our algorithm is prominent for block-structured adaptive mesh because
the matrix assembling occupies a very small portion of the total CPU time. This
method can be applied to solve the pressure equations for incompressible flows
by utilizing available highly efficient ‘black-box’ linear solvers.
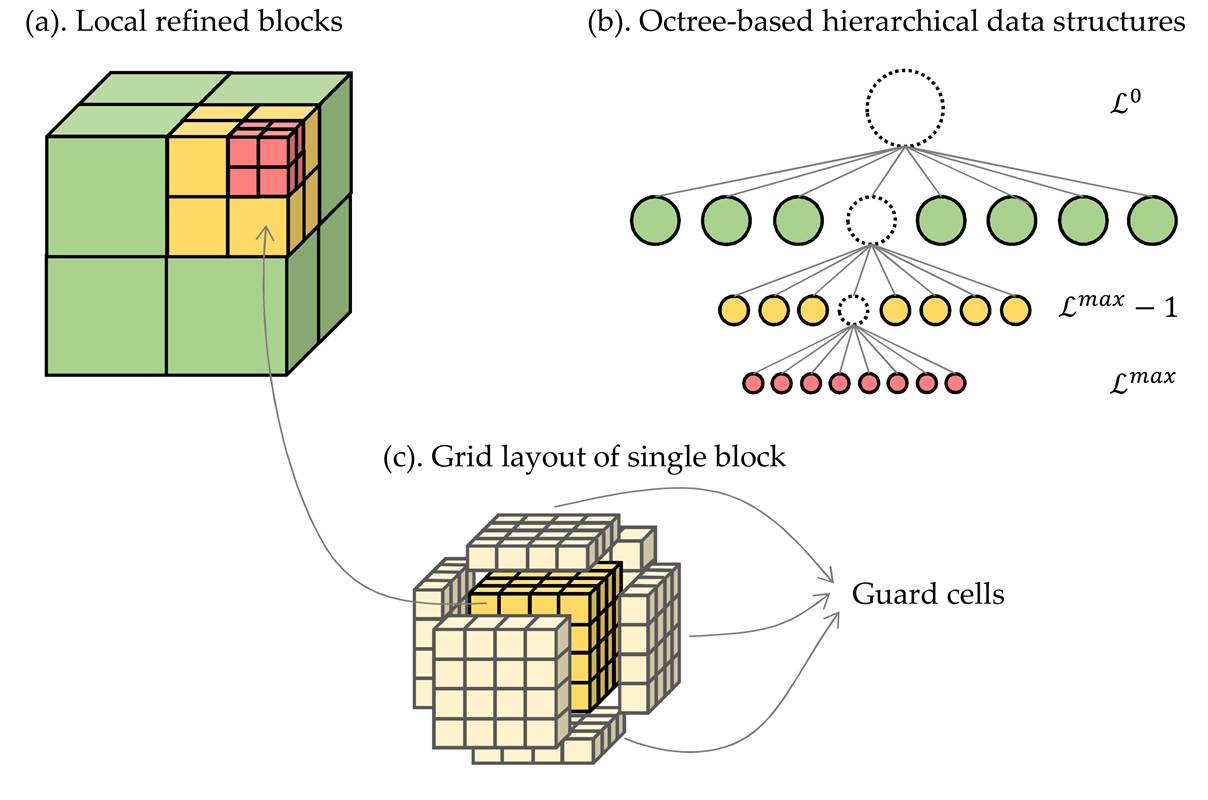
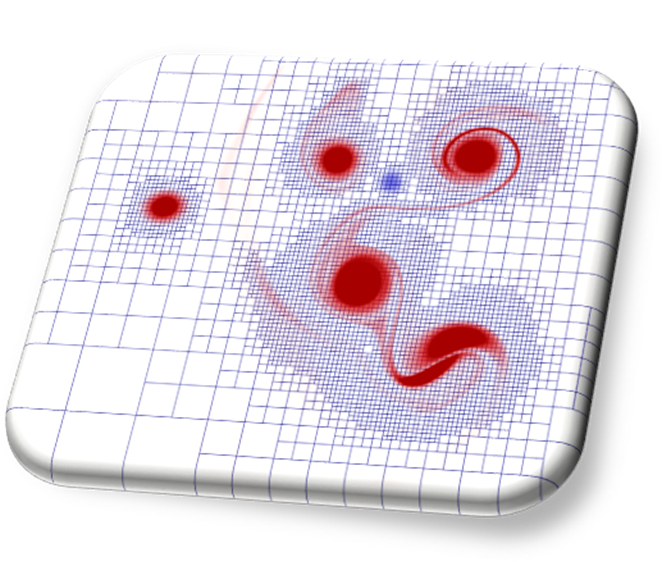
Fig. 1 3-D
adaptive mesh and its representation as an octree.
Flow past
circular cylinder
(a). 
(b). 
(c). 
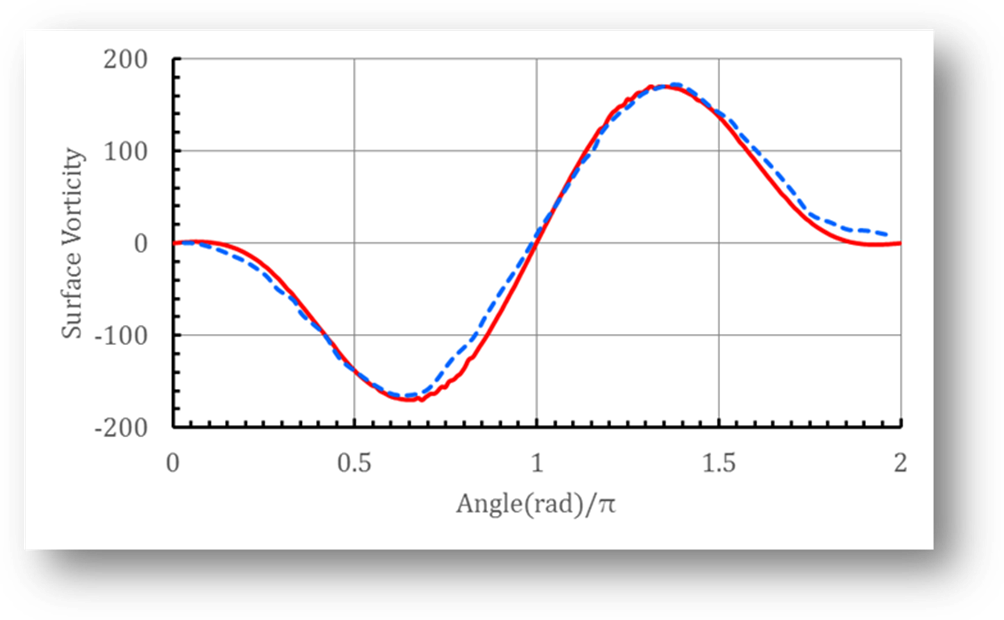
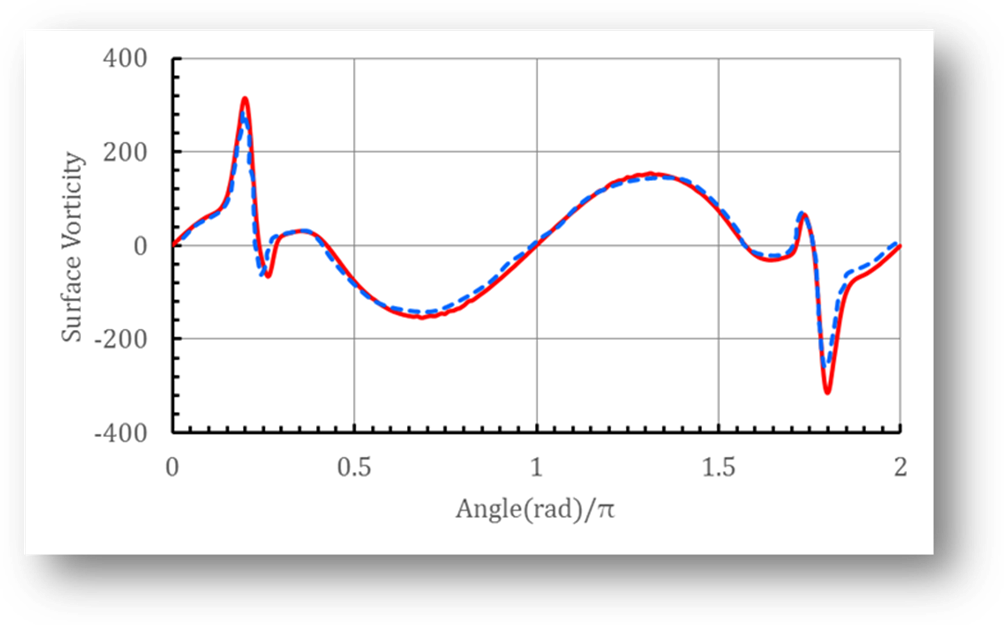
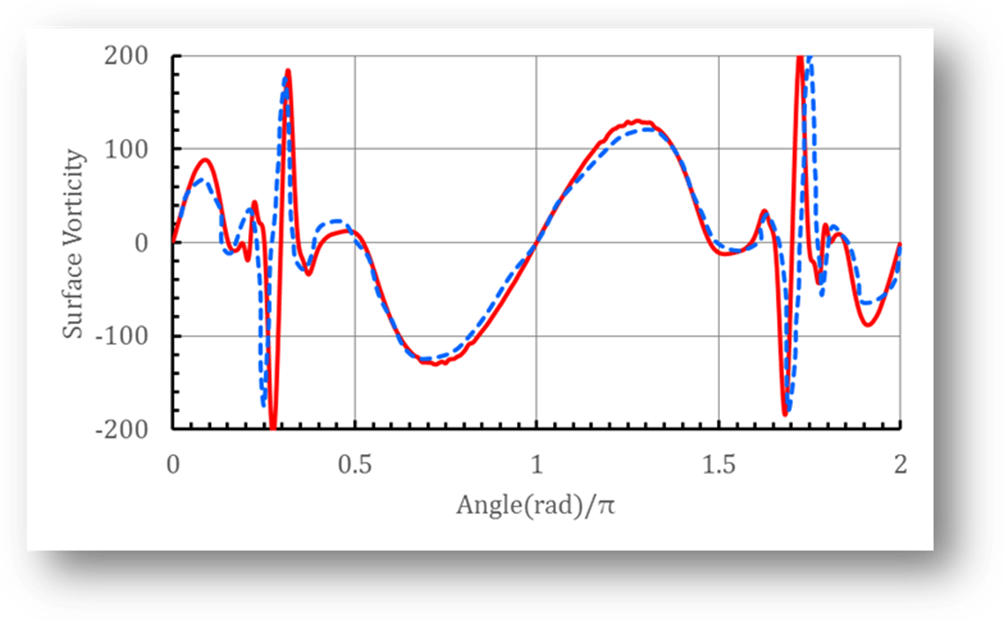
Fig. 2 Vorticity on the surface for Re=9500, ‑‐‐: results of P. Koumousatkos
et al. ; –: present
solution.
(a)
(b)
(c) 
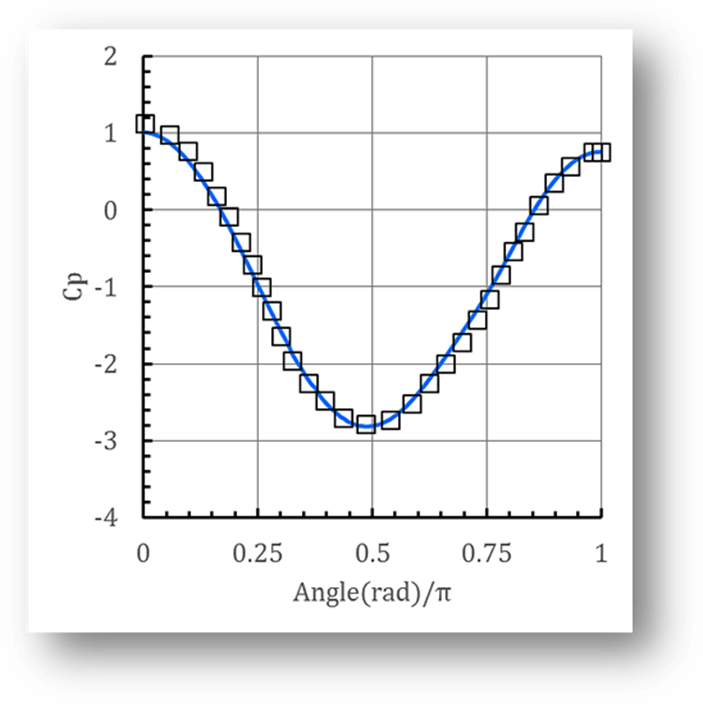
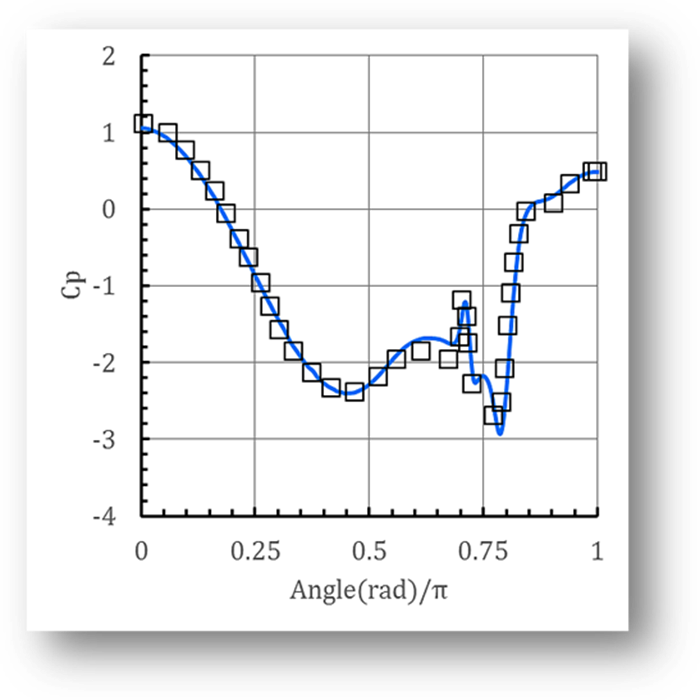
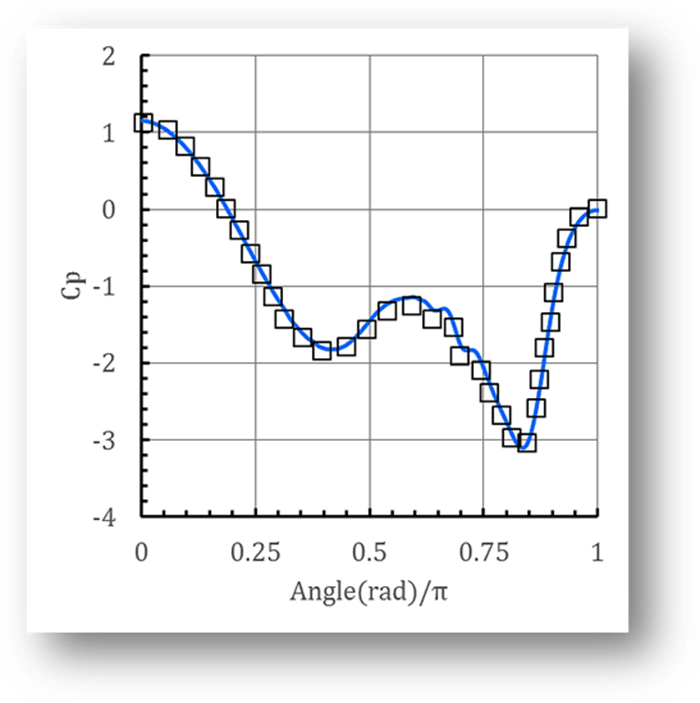
Fig. 3 Instantaneous pressure coefficients for
, □: results of J. C. Suh et al. ; –: present solution.
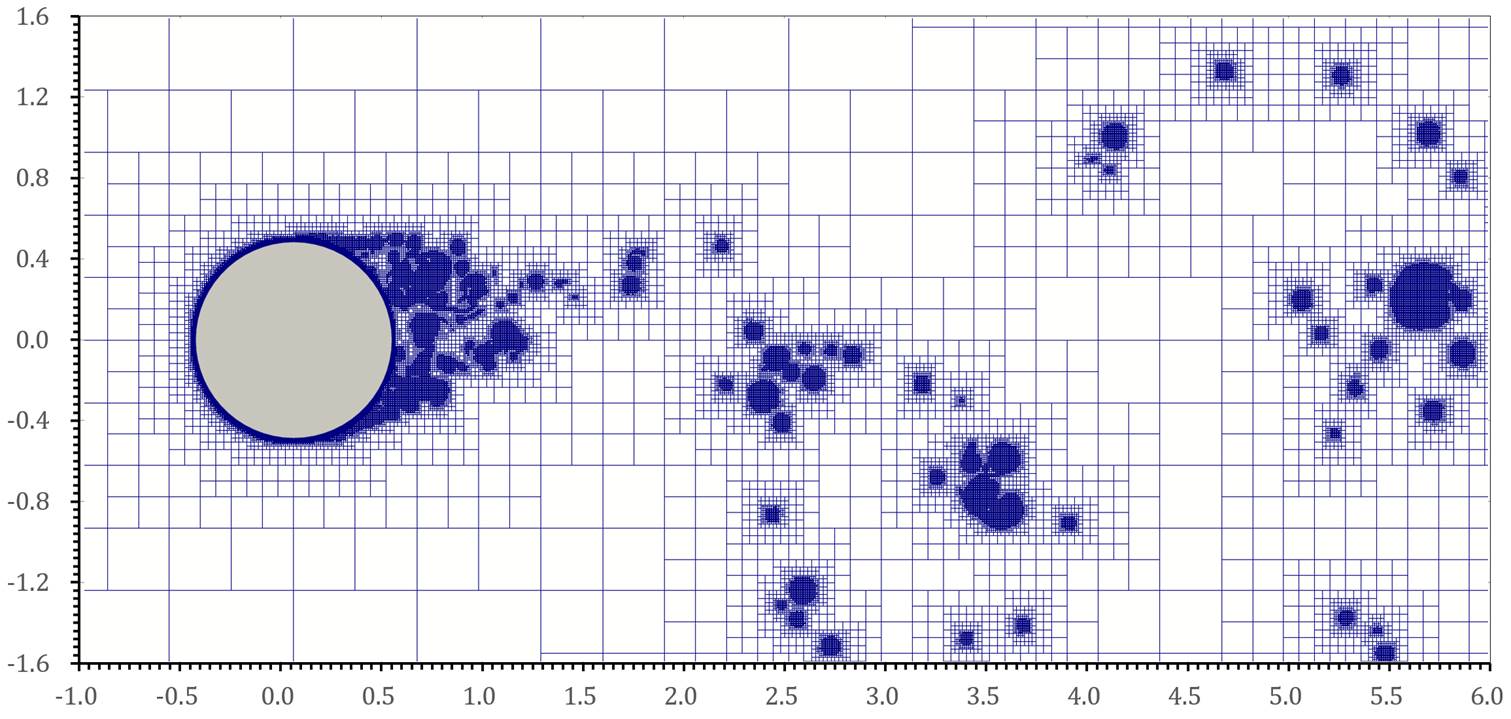
Fig. 4 Instantaneous blocks of flow past circular cylinder with 
(
), 10 mesh levels (level 4~14) are
used.
Flow past a rapidly
pitching NACA 0015 airfoil
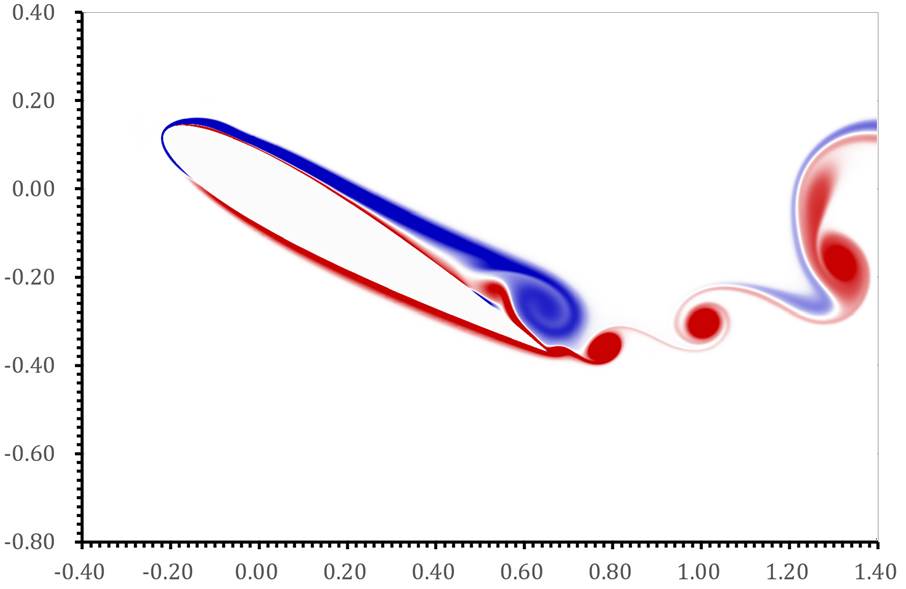
(a) 
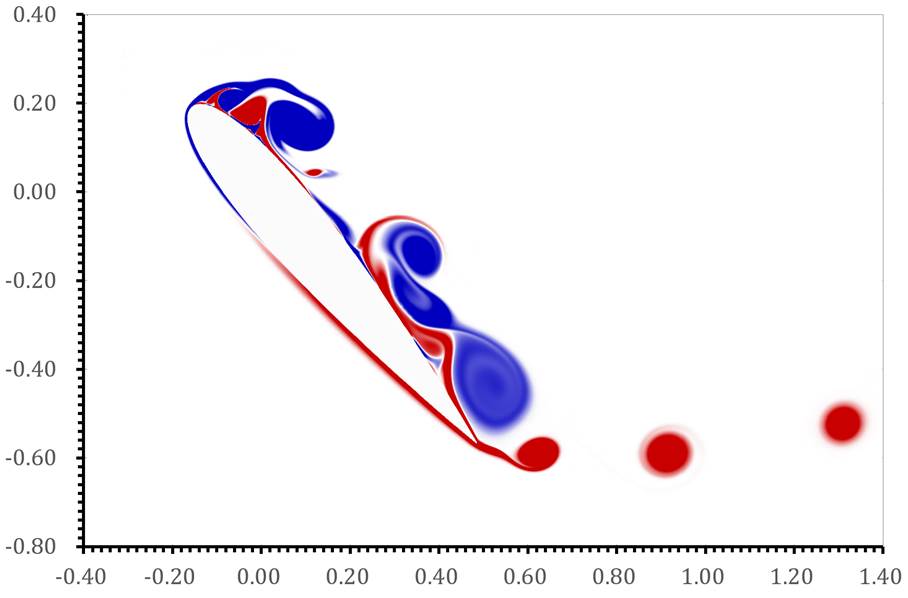
(b) 
Fig. 5 Vorticity field of fast pitching of NACA0015 under 
on different pitching angles.
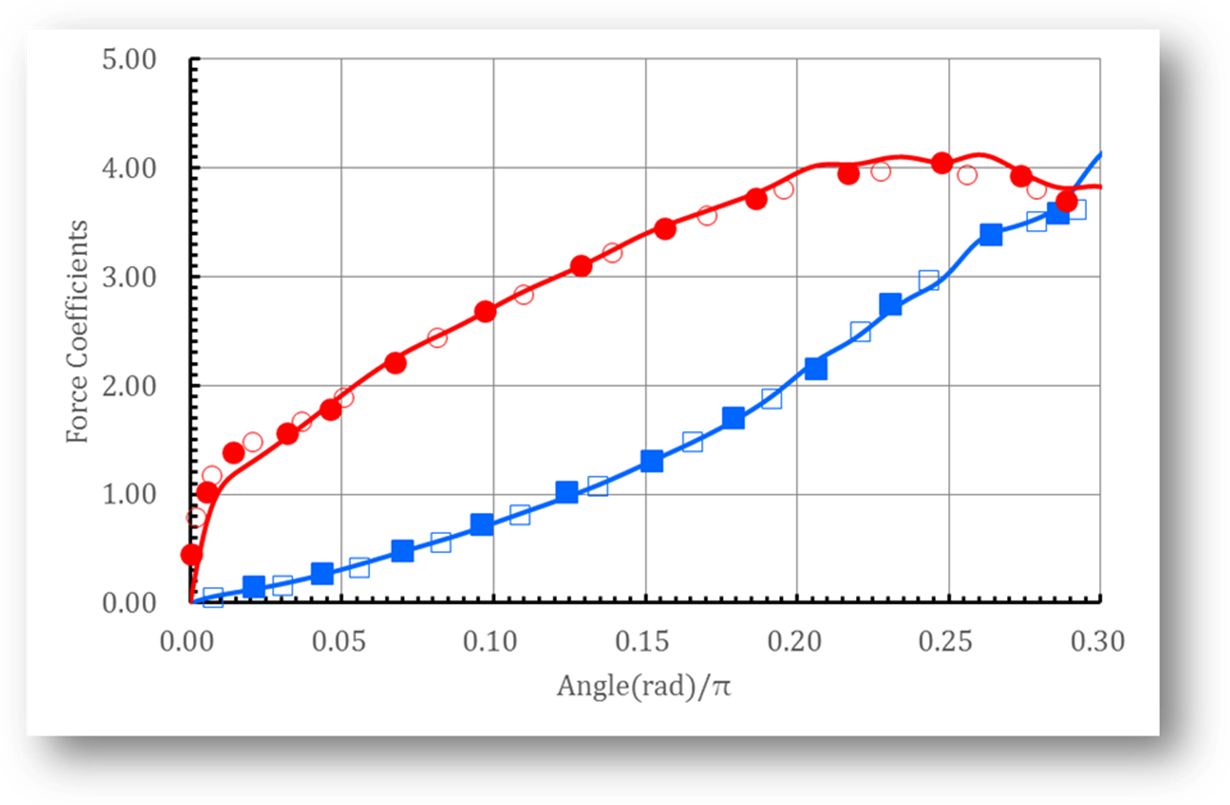
Fig. 6 Force coefficients of the fast pitching test for . –, –: present
and
, respectively; ■,●: 
and of M. R. Visbal
et al. ; □,○: and of I. Lomtev et
al.
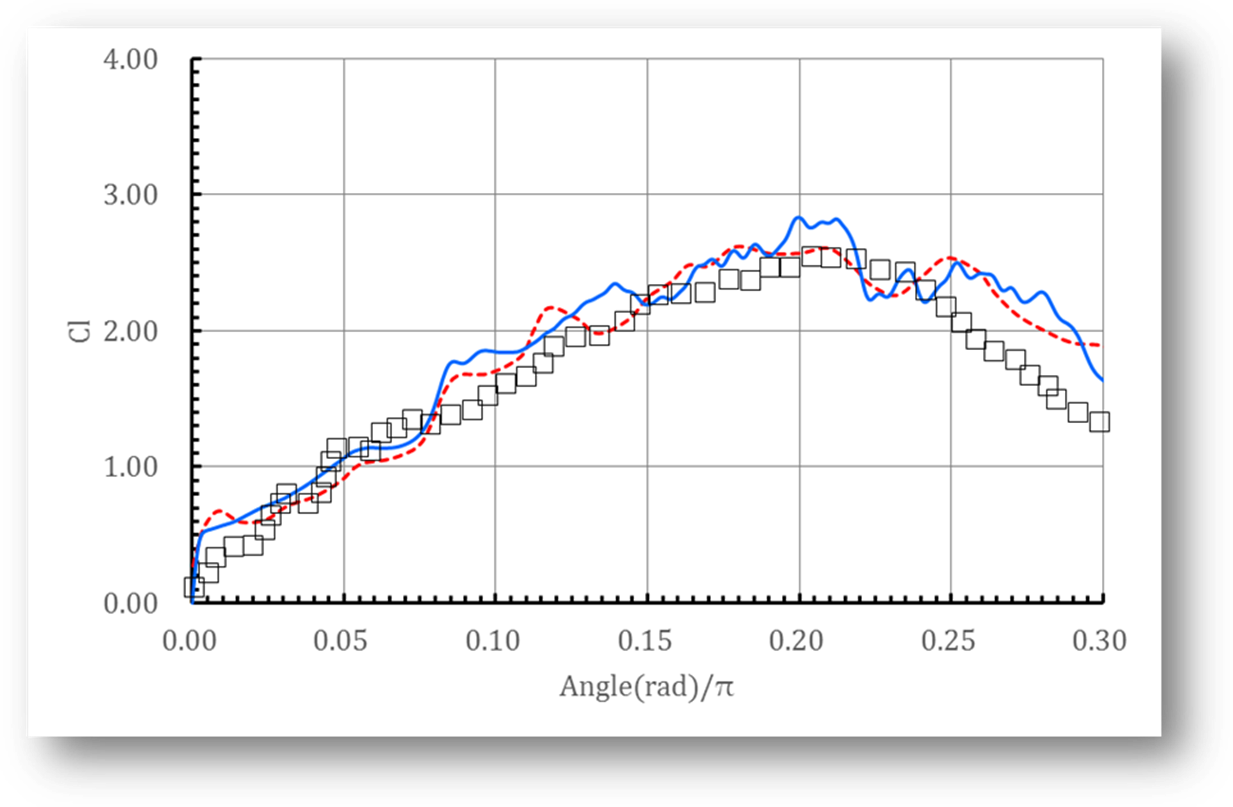
Fig. 7 Lift coefficients (
) of the fast pitching test for
. –: present numerical results; – –:
numerical solutions of M. R. Visbal et al. ; □: experimental results of H. E. Helin
et al..
Flow past a rapidly
pitching 3D thin plate
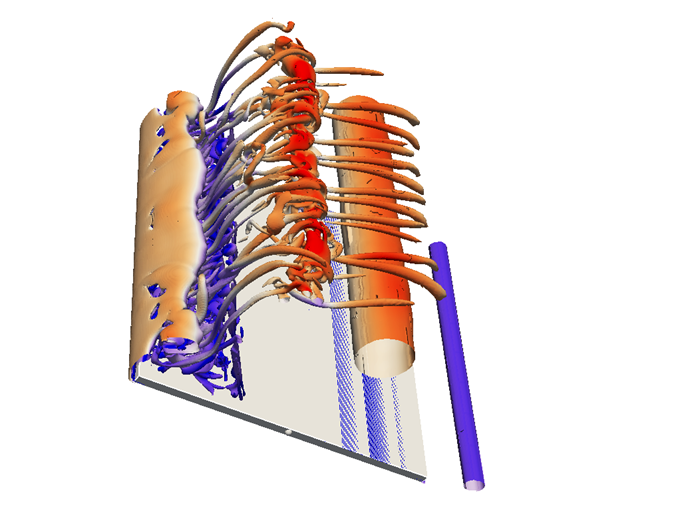
(a)
↑44.2°
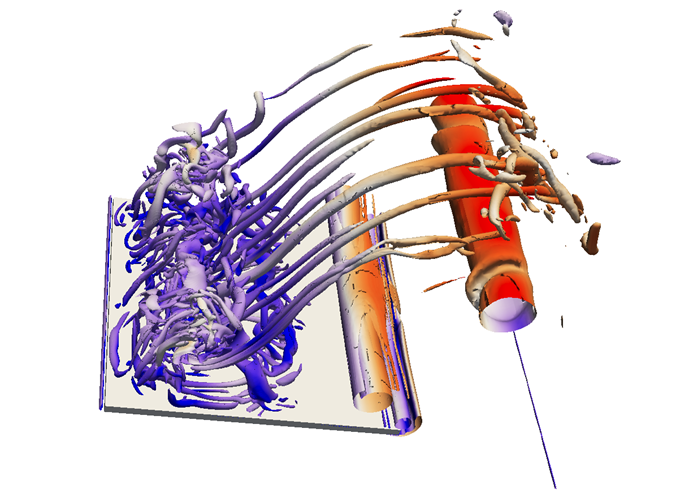
(b)
↓21.8°
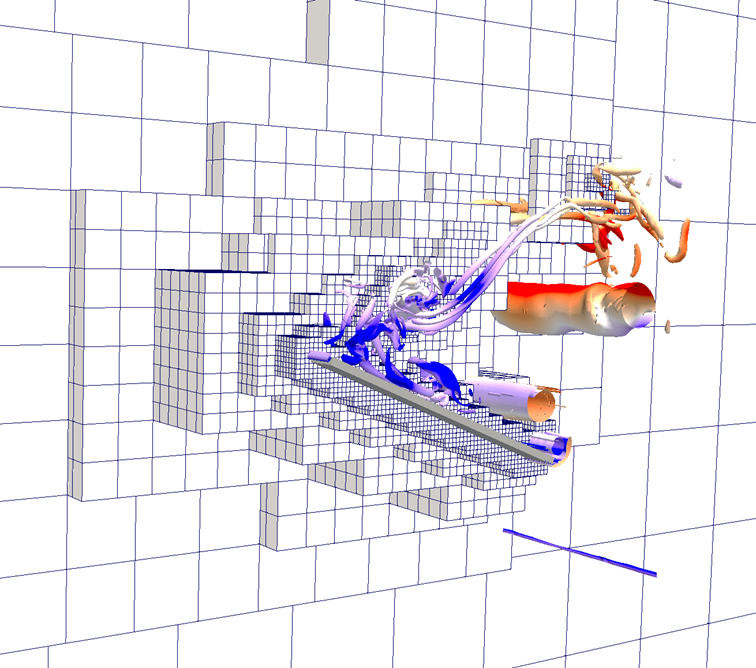
(c) 3D hierarchical blocks (level 2~7),
each block contains uniform
mesh.
Fig. 8 3D simulation of flow past rapidly
pitching thin plate, Q-criterion iso-surfaces of Motion-I.
Reference
C. Liu*, C.
Hu, An adaptive multi-moment FVM approach for incompressible flows, Journal
of Computational Physics, (2018) 359: 239-262.