Elliptic Problems

A second order Ghost Fluid method is proposed for the treatment of interface problems of elliptic equations with discontinuous coefficients. By appropriate use of auxiliary virtual points, physical jump conditions are enforced at the interface. The signed distance function is used for the implicit description of irregular domain. With the additional unknowns, high order approximation considering the discontinuity can be built. To avoid the ill-conditioned matrix, the interpolation stencils are selected adaptively to balance the accuracy and the numerical stability. Additional equations containing the jump restrictions are assembled with the original discretized algebraic equations to form a new sparse linear system. Several Krylov iterative solvers are tested for the newly derived linear system.

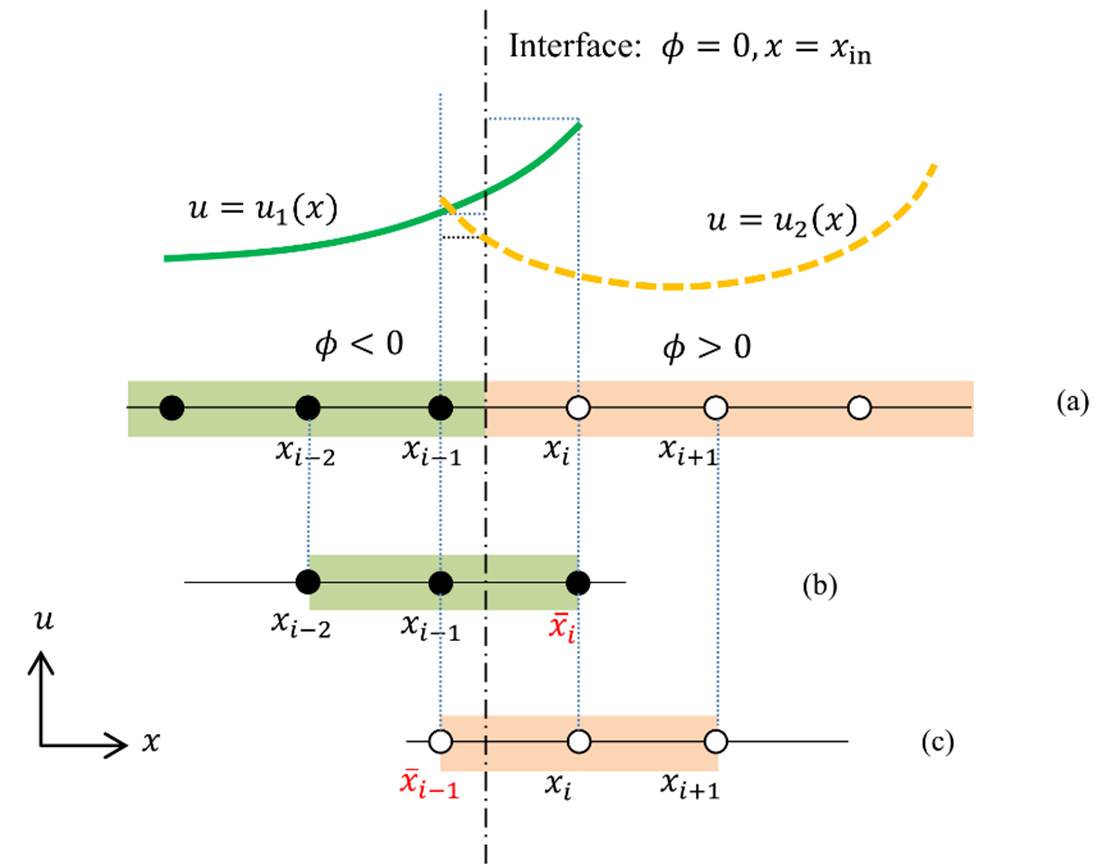
Fig. 1 One dimensional interpolation scheme for jump conditions.

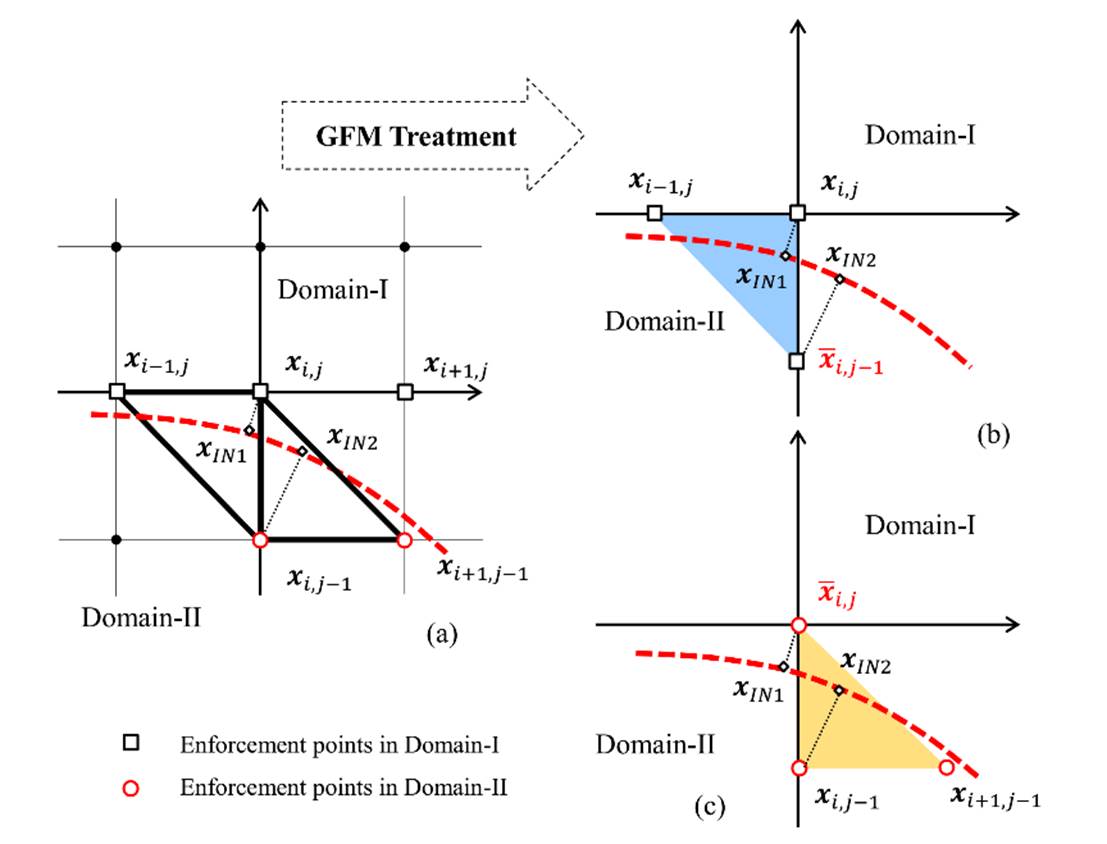
Fig. 2 Classification of the points for construction of jump conditions. (a) Original enforcing points of the two domains, (b) Interpolation stencils for domain-I, (c) interpolation stencils for domain-II.

Table. 1 Average errorand maximum error.

Present GFM method				Previous GFM method (Liu and Fedkiw, 2000)
error	order	error	order	error	order	error	order
2.8790E-3	-	5.8066E-4	-	1.5300E-2	-	5.4000E-3	-
5.5882E-4	1.932	1.4639E-4	1.992	8.1000E-3	0.920	2.2000E-3	1.300
1.3707E-4	2.019	4.0393E-5	1.904	4.4000E-3	0.880	9.0000E-4	1.290
4.0929E-5	1.830	1.0532E-5	1.958	2.3000E-3	0.940	3.0000E-4	1.590

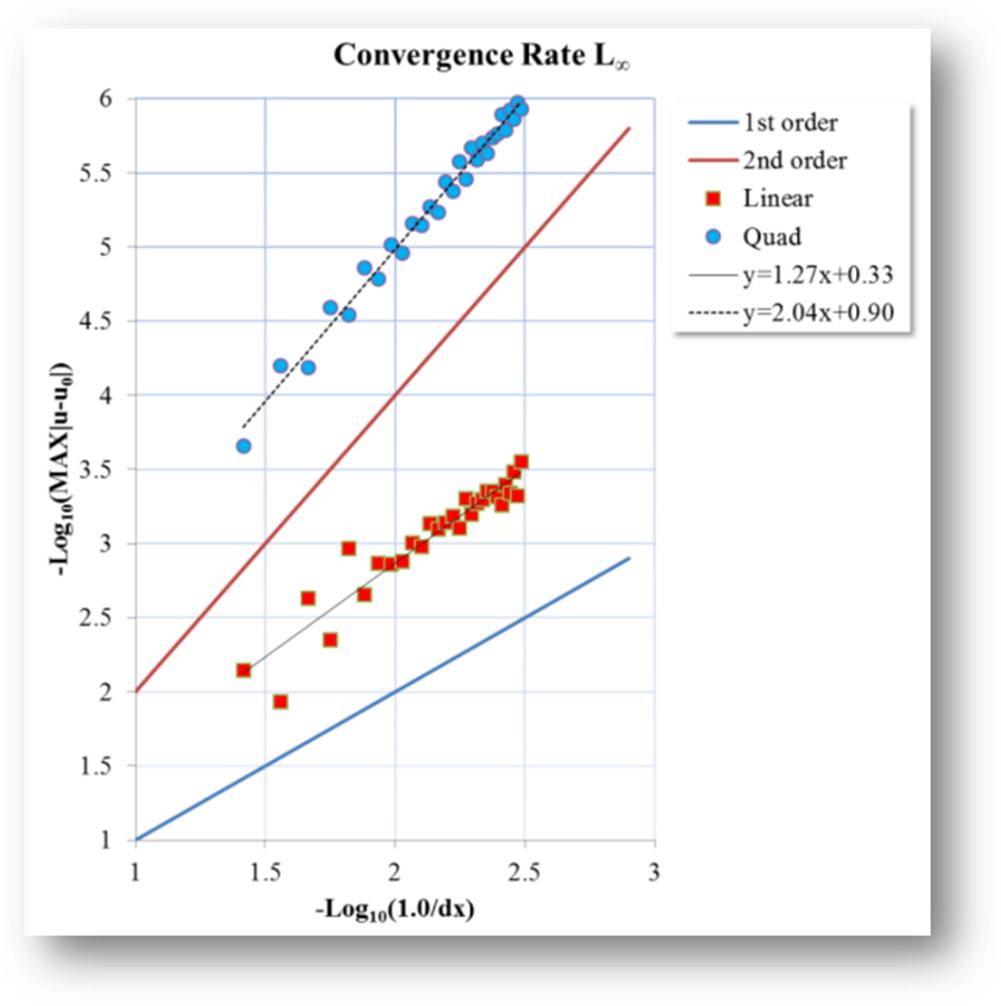
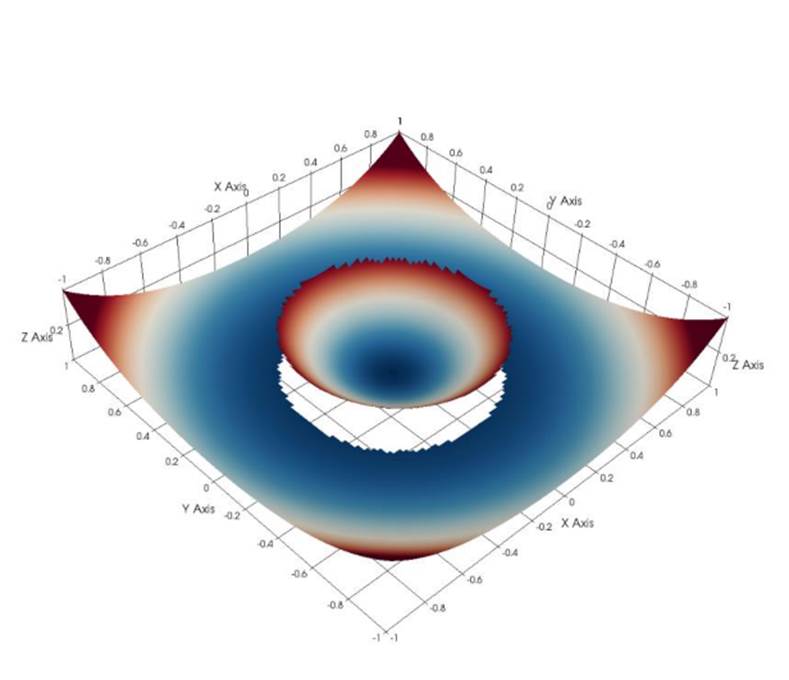
Fig. 3 Numerical accuracy tests for an elliptic problem.

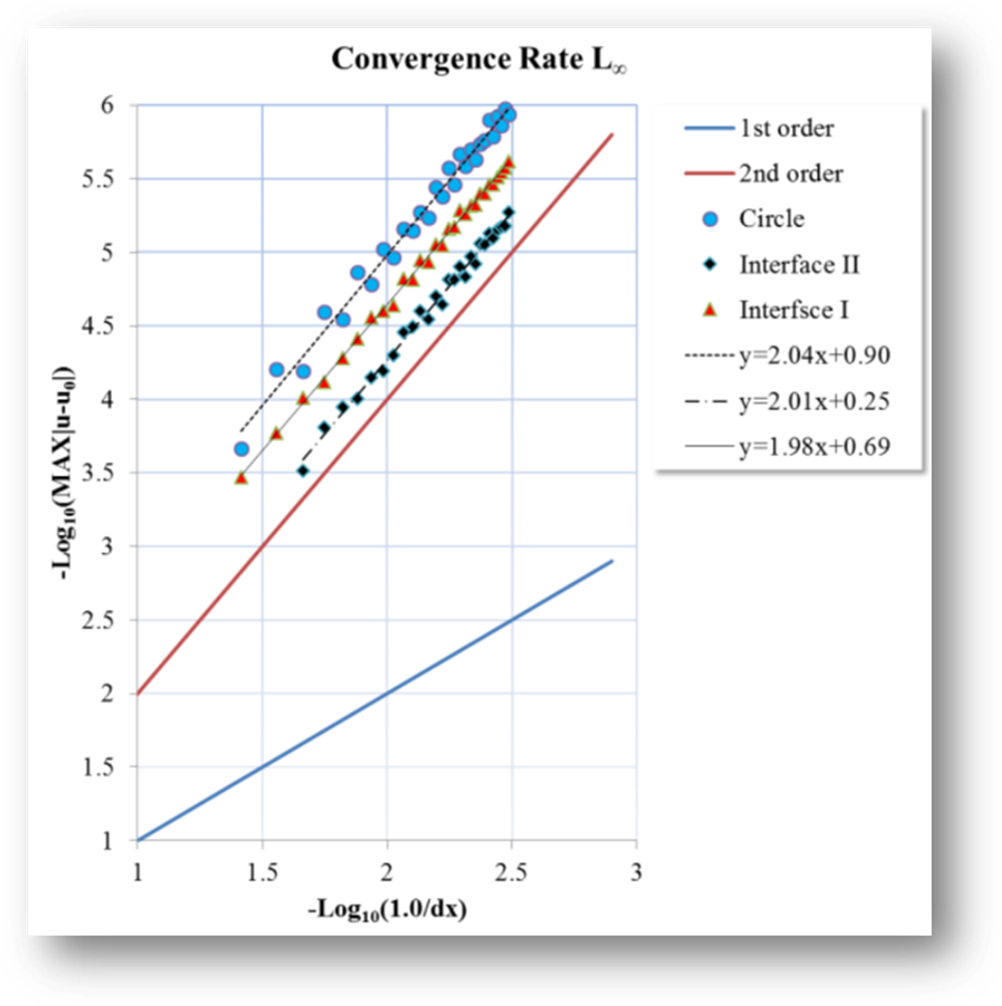
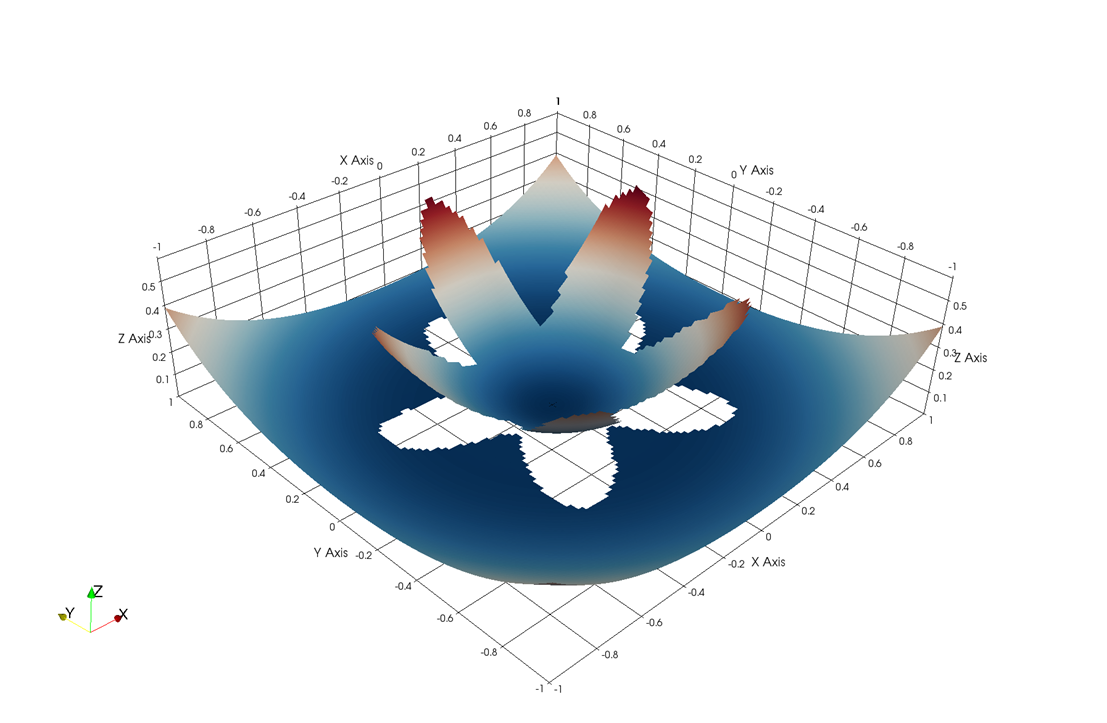
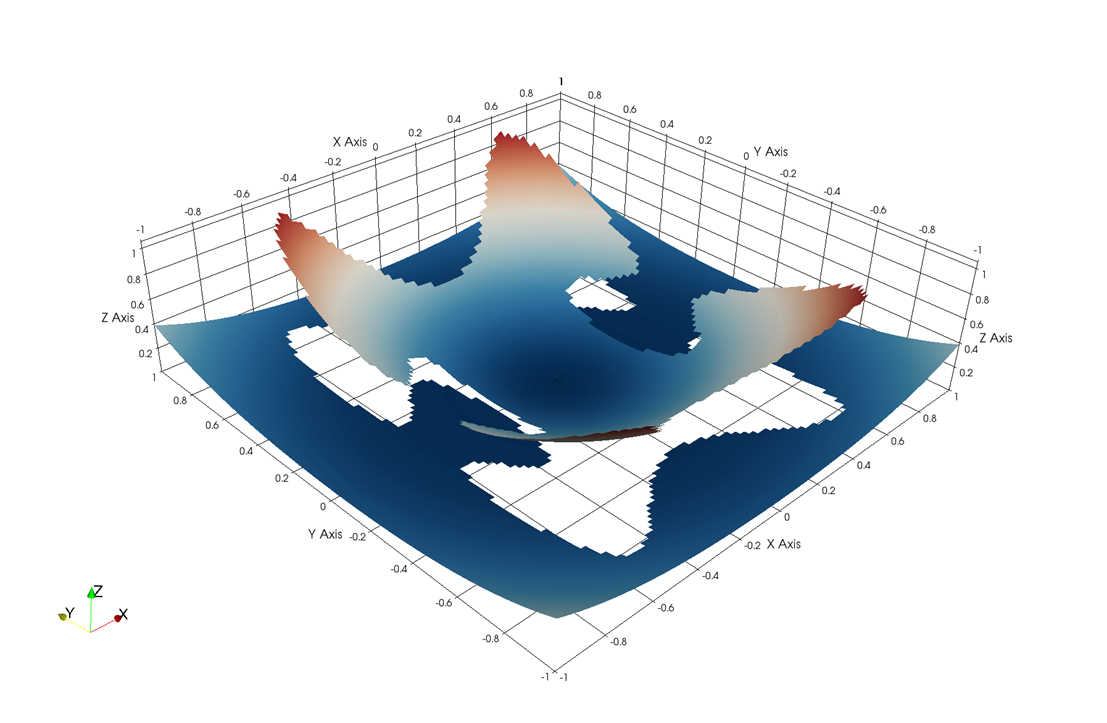
Fig. 4 Numerical accuracy tests for two elliptic problem with irregular interface shape.

GFM for Two Phase Flows (Sharp Interface Method)

Droplet Impaction

Reference

C. Liu*, C. Hu, A Second Order Ghost Fluid Method for an Interface Problem of the Poisson Equation, Communications in Computational Physics, (2017), 22(4): 965-996.

Return to homepage