Immersed
Boundary Method
An efficient
immersed boundary treatment for simulation of flexible moving body immersed in
fluid is presented. The level set signed distance function is used to indicate
body surface. A
simple mapping strategy is proposed to avoid costly signed distance
re-initialization computations. The strategy is efficient for both rigid and
deformable structures, and can be extended to 3-D case easily. With the use of
signed distance function, reconstruction of flow variables on a body
surface can be easily implemented through linear, bilinear or quadratic
interpolation. In order to suppress the pressure oscillations caused by the
role conversion of forcing points and fluid points, a modified interpolation
scheme is presented by introducing a dynamic weight term to the fluid point.
Together with local grid refinement and using larger time step, the pressure
oscillations can be effectively diminished by the modified interpolation scheme.
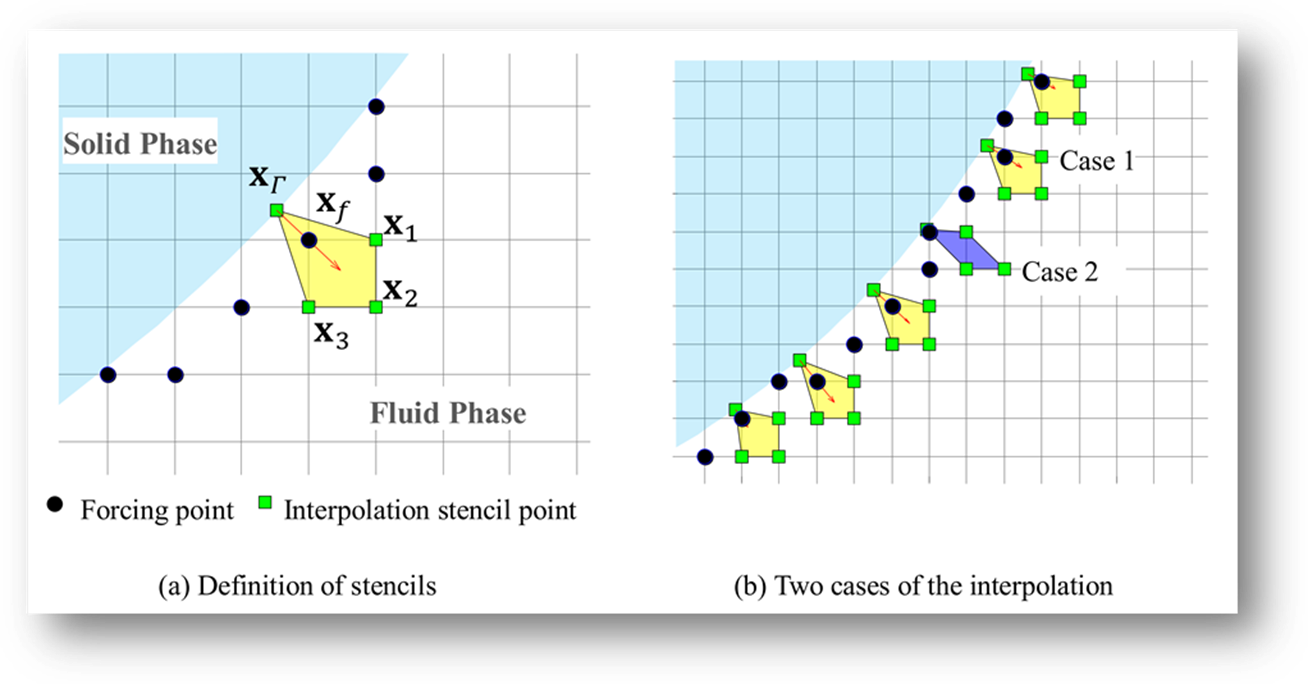
Fig. 1.
Stencils for
bilinear interpolation.
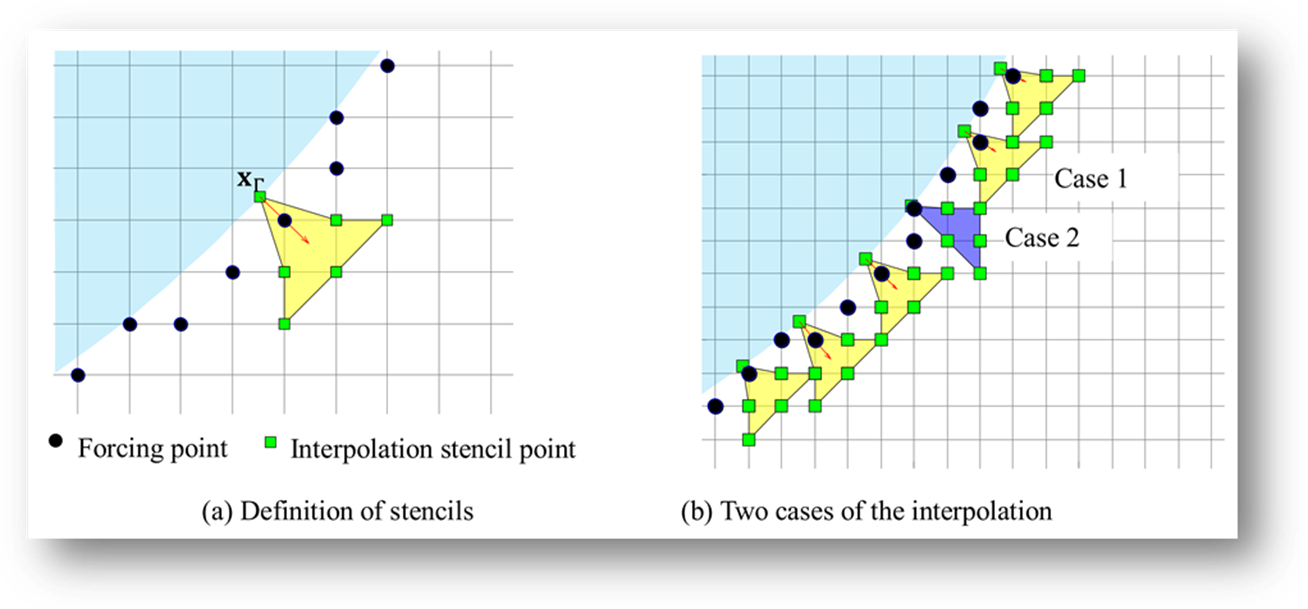
Fig. 2. Stencils
for quadratic interpolation.
In-line oscillating cylinder
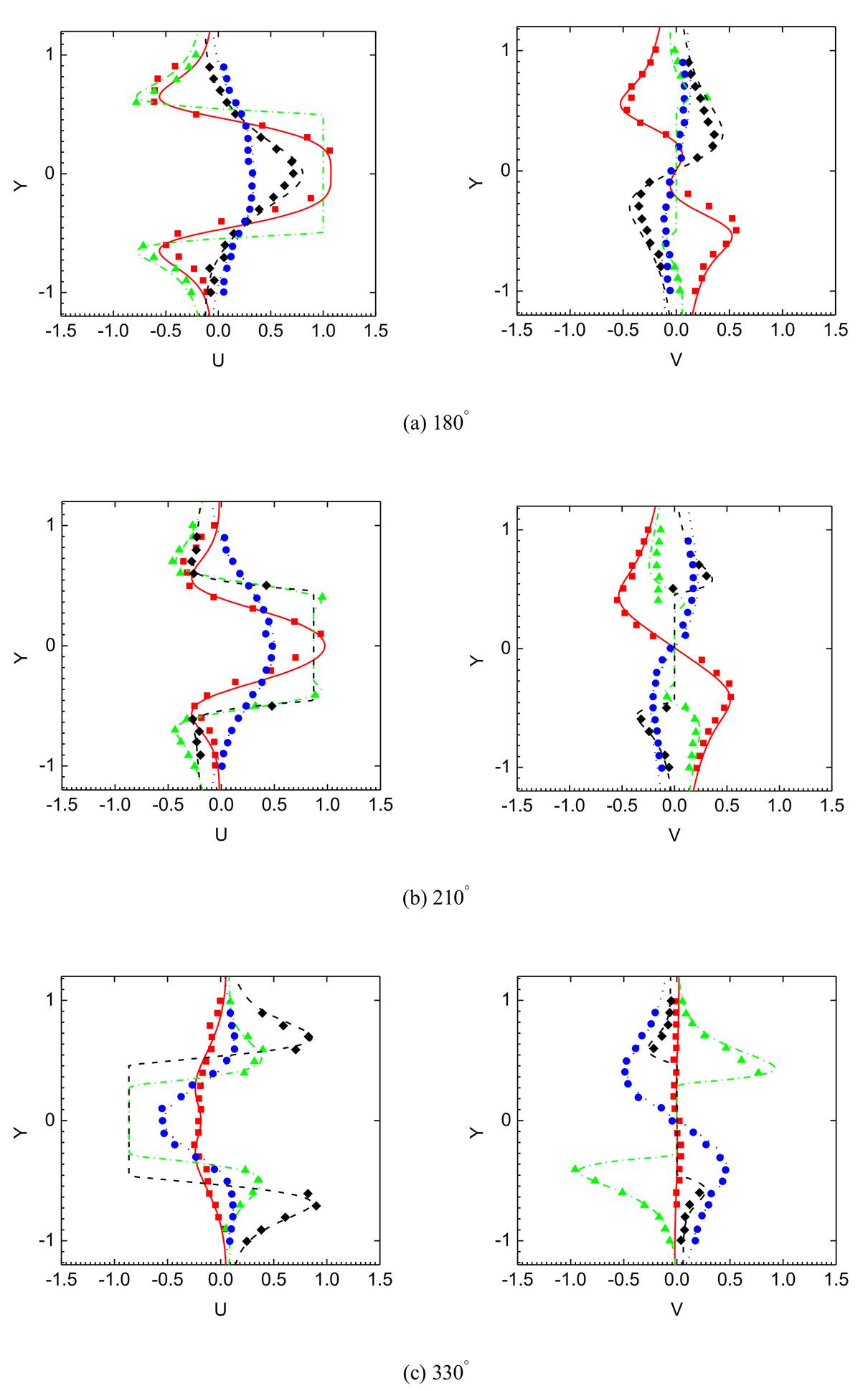
Fig.
3. Comparison of the present numerical
result (indicated with lines,··· : x=1.2D, ─ : x=-0.6D, ─·─· : x=0D,─ ─ : x=0.6D) and experimental result of Du¨tsch (indicate by solid marks, ●: x=1.2D,
■: x=-0.6D, ▲: x=0D,
◆: x=0.6D) in different phase positions.
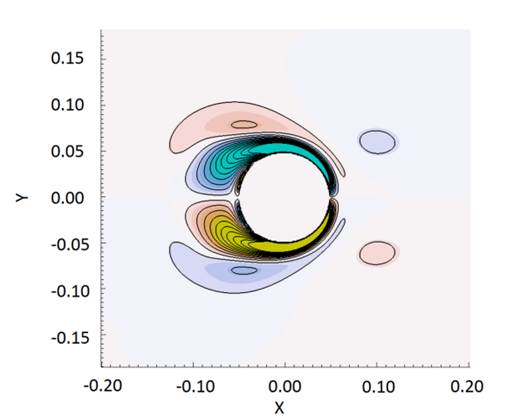
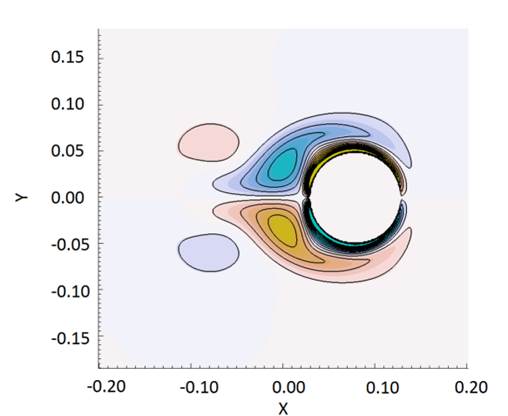
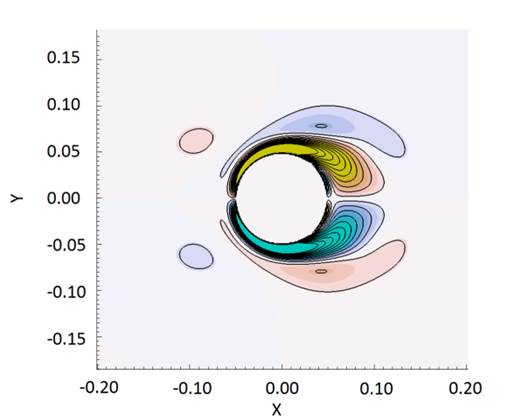
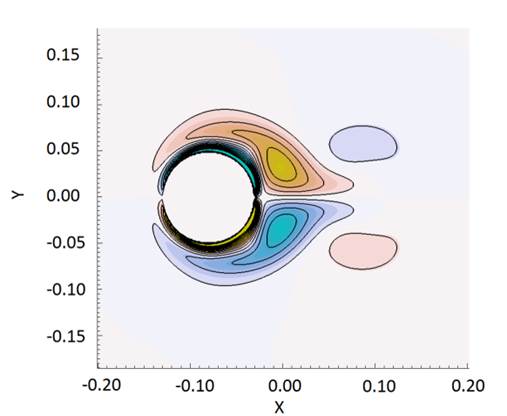
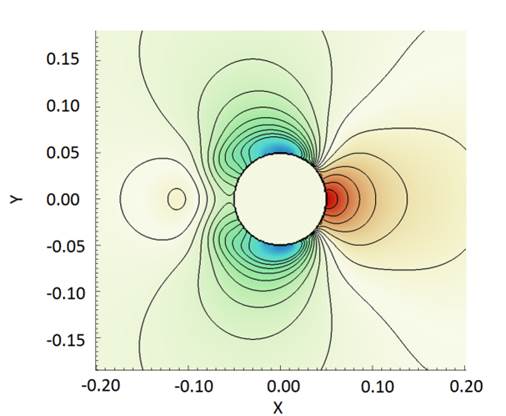
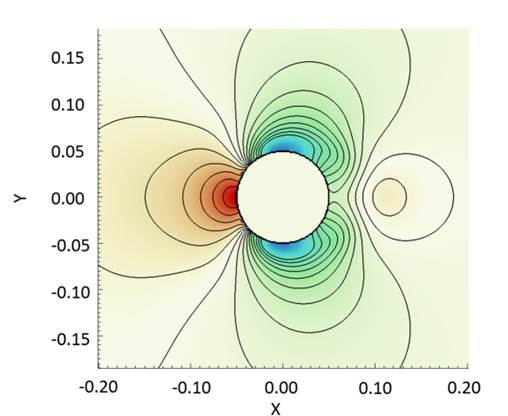
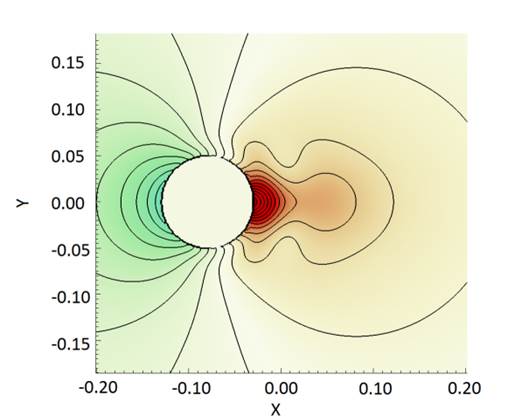
Fig.
4. Computed streamline together with
pressure distribution and vorticity contours of in-line oscillation in phase
position.
Transversely oscillating cylinder
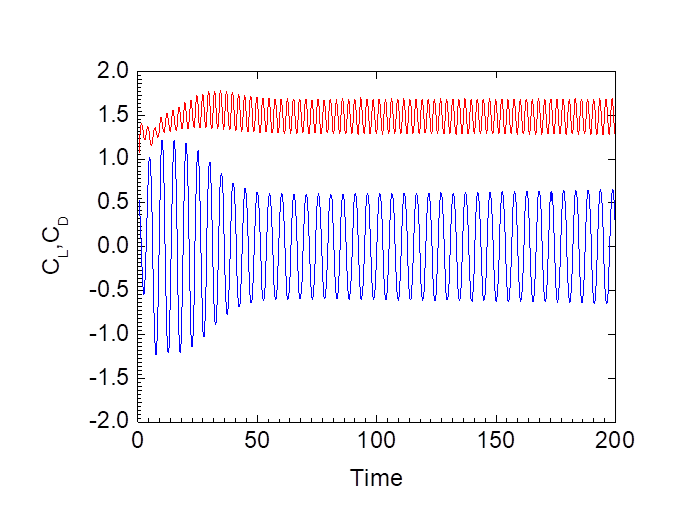
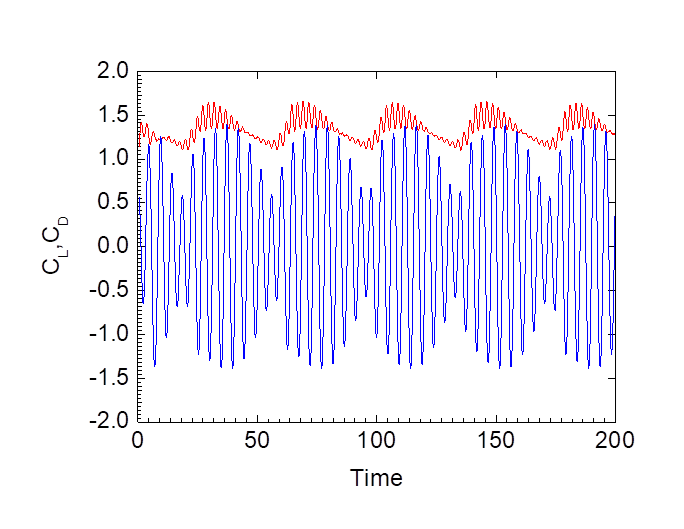
Fig. 5
Time evolution of the lift and drag coefficient for transversely oscillation
case (
,
).
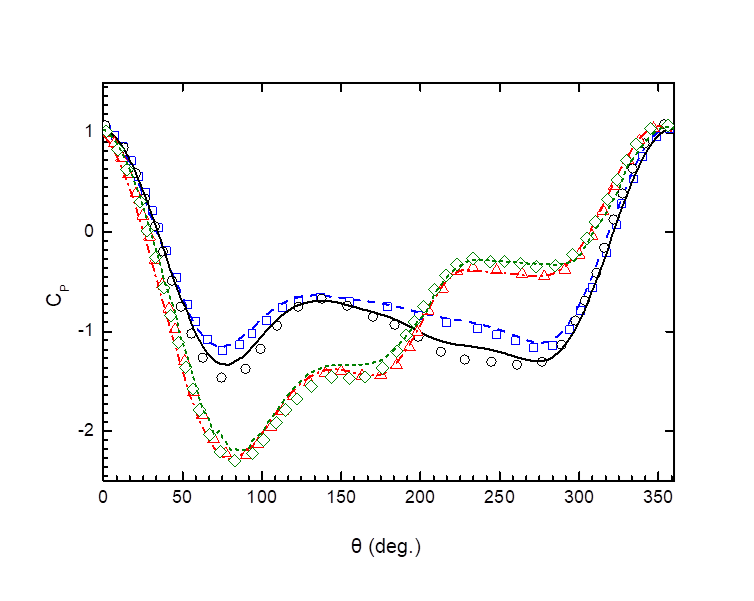
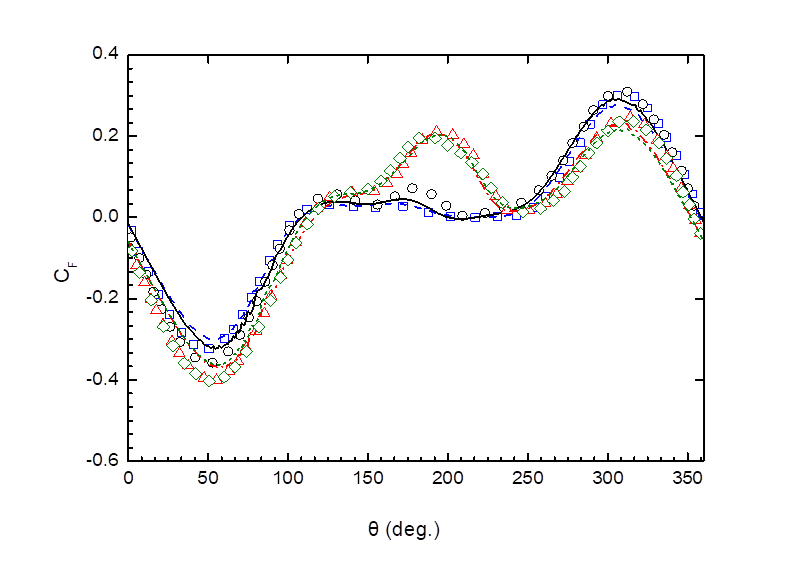
Fig. 6 Force
coefficients
on the cylinder surface with line
indicating present results and markers the results by body fitted method (□, ─ ─: 
; ○, ──:
; △, ─ · ─:; ◇, - - -:
).
Anguilliform swimmer in fluid
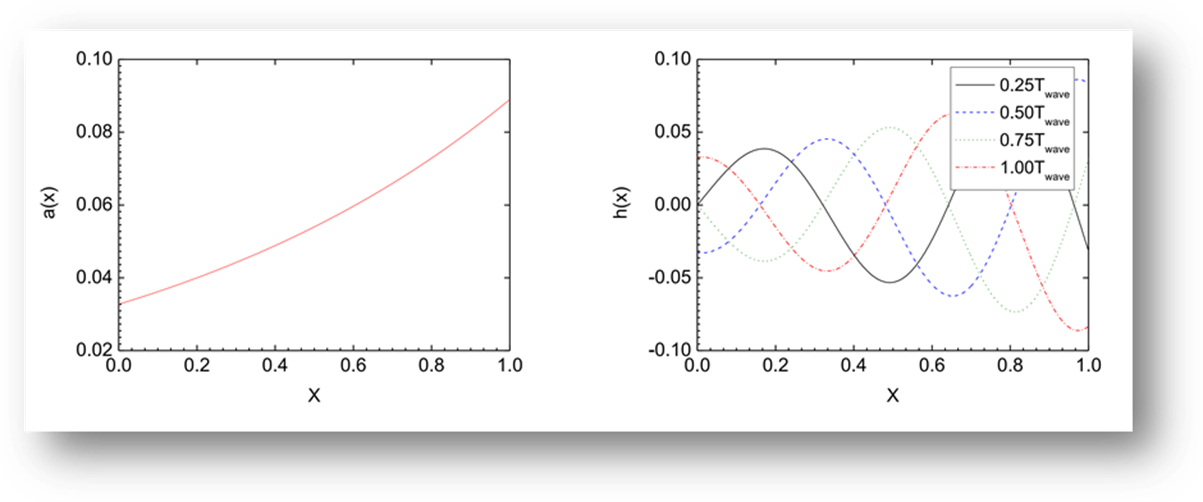
Fig. 7
Amplitude envelops and lateral undulation profile of
the anguilliform swimmer.
Fig. 8 Vortex
structure visualized by q-criterion for anguilliform swimmer at 
and different Strouhal
numbers (left, St=0.2; right, St=0.7).
Fig. 9 Pressure
contours for anguilliform swimmer at with St=0.7.
Reference
C. Liu, C.
Hu*, An efficient immersed boundary treatment for complex moving object, Journal
of Computational Physics, (2014), 274: 654-680.
C. Hu, C. Liu, Improvement of Immersed Boundary
Method for Simulation of Fluid-Structure Interaction, The 31th Intentional
Workshop on Water Waves and Floating Bodies, Michigan, USA, 2016.
C. Liu, C.
Hu, An Immersed Boundary Method for Simulating of Flow with Moving Body, The 27th
Computational Fluid Dynamics Symposium (第27回数値流体力学シンポジウム),
Nagoya, Japan, 2013.